练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在一次期末数学测试中，唐老师任教班级学生的考试得分情况如表所示：

    分数区间

    人数

    2

    8

    32

    38

    20

    （1）根据上述表格，试估计唐老师所任教班级的学生在本次期末数学测试的平均成绩；

    （2）现从成绩在中按照分数段，采取分层抽样的方法随机抽取5人，再在这5人中随机抽取2人作小题得分分析，求恰有1人的成绩在上的概率.

    【答案】（1）；（2）

    【解析】

    (1)利用表格中给出的数据即可求出平均成绩；

    (2)本题首先可以根据分层抽样的定义得出和两个分数段中抽取的人数，然后列出随机抽取2人的所有基本事件，最后找出满足恰有1人的成绩在上的基本事件，即可得出结果.

    (1)依题意，所求平均成绩为

    .

    (2)依题意，由分层抽样方法知的抽取1人，记为a，抽取4人，

    记为A，B，C，D，则抽取2人，所有情况为：

    ,，共10种，

    其中满足条件的有：，共4种，

    所以恰有1人的成绩在上的概率为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某人经营淡水池塘养草鱼，根据过去期的养殖档案，该池塘的养殖重量(百斤)都在百斤以上，其中不足百斤的期，不低于百斤且不超过百斤的有期，超过百斤的有期.根据统计，该池塘的草鱼重量的增加量(百斤)与使用某种饵料的质量(百斤)之间的关系如图所示.

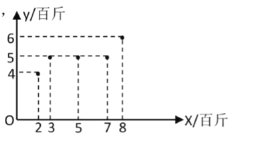
    鱼的重量(单位:百斤)

    冲水机运行台数

    1

    2

    3

    （1）根据数据可知与具有线性相关关系，请建立关于的回归方程；如果此人设想使用某种饵料百斤时，草鱼重量的增加量须多于百斤，请根据回归方程计算，确定此方案是否可行？并说明理由.

    （2）养鱼的池塘对水质含氧与新鲜度要求较高，故养殖户需设置若干台增氧冲水机，每期养殖使用的冲水机运行台数与鱼塘的鱼重量有关，并有如下关系:

    若某台增氧冲水机运行，则该台冲水机每期盈利千元；若某台冲水机未运行，则该台冲水机每期亏损千元.以频率 作为概率，养殖户欲使每期冲水机总利润的均值达到最大，应安装几台增氧冲水机？

    附:对于一组数据，其回归方程的斜率和截距的最小二乘估计公式分别为:，.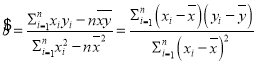

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商家统计了去年，两种产品的月销售额（单位：万元），绘制了月销售额的雷达图，图中点表示产品2月份销售额约为20万元，点表示产品9月份销售额约为25万元.

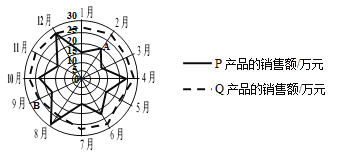
    根据图中信息，下面统计结论错误的是（ ）

    A.产品的销售额极差较大B.产品销售额的中位数较大

    C.产品的销售额平均值较大D.产品的销售额波动较小

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在某区“创文明城区”简称“创城”活动中，教委对本区A，B，C，D四所高中校按各校人数分层抽样调查，将调查情况进行整理后制成如表：

    学校

    A

    B

    C

    D

    抽查人数

    50

    15

    10

    25

    “创城”活动中参与的人数

    40

    10

    9

    15

    注：参与率是指：一所学校“创城”活动中参与的人数与被抽查人数的比值

    假设每名高中学生是否参与“创城”活动是相互独立的．

    Ⅰ若该区共2000名高中学生，估计A学校参与“创城”活动的人数；

    Ⅱ在随机抽查的100名高中学生中，从A，C两学校抽出的高中学生中各随机抽取1名学生，求恰有1人参与“创城”活动的概率；

    Ⅲ若将表中的参与率视为概率，从A学校高中学生中随机抽取3人，求这3人参与“创城”活动人数的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】平面直角坐标系中，过椭圆： （）焦点的直线交于两点， 为的中点，且的斜率为9.

    （Ⅰ）求的方程；

    （Ⅱ）是的左、右顶点， 是上的两点，若，求四边形面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某超市从年甲、乙两种酸奶的日销售量（单位：箱）的数据中分别随机抽取个，并按、、、、分组，得到频率分布直方图如图，假设甲、乙两种酸奶独立销售且日销售量相互独立.

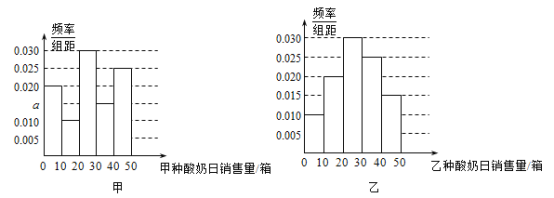
    （1）写出频率分布直方图甲中的的值；记甲种酸奶与乙种酸奶日销售量（单位：箱）的方差分别为、，试比较与的大小；（只需写出结论）

    （2）估计在未来的某一天里，甲、乙两种酸奶的销售量恰有一个高于箱且另一个不高于箱的概率；

    （3）设表示在未来天内甲种酸奶的日销售量不高于箱的天数，以日留住量落入各组的频率为概率，求的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】四棱锥的底面是正方形，平面，且，该四棱锥的五个顶点都在同一个球面上，分别是棱的中点，直线被球面所截得的线段长为，则该球的表面积为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】求矩阵M＝的特征值和特征向量．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年7曰1日至3日，世界新能源汽车大会在海南博鳌召开，大会着眼于全球汽车产业的转型升级和生态环境的持续改善.某汽车公司顺应时代潮流，最新研发了一款新能源汽车，并在出厂前对100辆汽车进行了单次最大续航里程（理论上是指新能源汽车所装载的燃料或电池所能够提供给车行驶的最远里程）的测试.现对测试数据进行分析，得到如下的频率分布直方图：

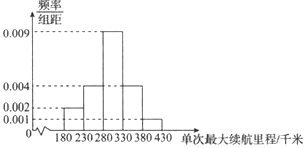
    （1）估计这100辆汽车的单次最大续航里程的平均值（同一组中的数据用该组区间的中点值代表）.

    （2）根据大量的汽车测试数据，可以认为这款汽车的单次最大续航里程近似地服从正态分布，经计算第（1）问中样本标准差的近似值为50.用样本平均数作为的近似值，用样本标准差作为的估计值，现任取一辆汽车，求它的单次最大续航里程恰在250千米到400千米之间的概率.

    参考数据：若随机变量ξ服从正态分布，则，，.

    （3）某汽车销售公司为推广此款新能源汽车，现面向意向客户推出“玩游戏，送大奖”活动，客户可根据抛掷硬币的结果，操控微型遥控车在方格图上行进，若遥控车最终停在“胜利大本营”，则可获得购车优惠券.已知硬币出现正、反面的概率都是，方格图上标有第0格、第1格、第2格、…、第50格.遥控车开始在第0格，客户每掷一次硬币，遥控车车向前移动一次，若掷出正面，遥控车向前移动一格（从到），若掷出反面，遥控车向前移动两格（从到），直到遥控车移到第49格（胜利大本营）或第50格（失败大本营）时，游戏结束，设遥控车移到第n格的概率为，试说明是等比数列，并解释此方案能否成功吸引顾客购买该款新能源汽车.

    查看答案和解析>>

    同步练习册答案