
【题目】选修4—4:坐标系与参数方程
已知直线l经过点![]() ,倾斜角
,倾斜角![]() ,圆
,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出直线l的参数方程,并把圆![]() 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(Ⅱ)设l与圆![]() 相交于
相交于![]() 两点,求点
两点,求点![]() 到
到![]() 两点的距离之积.
两点的距离之积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由参数方程的概念可以写成l的参数方程为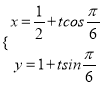 ,化简为
,化简为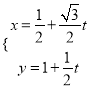 (t为参数) ;在
(t为参数) ;在![]() 两边同时乘以
两边同时乘以![]() ,且ρ2=x2+y2,ρcosθ=x,ρsinθ=y,∴
,且ρ2=x2+y2,ρcosθ=x,ρsinθ=y,∴![]() .(2)在l取一点,用参数形式表示
.(2)在l取一点,用参数形式表示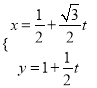 ,再代入
,再代入![]() ,得到t2+
,得到t2+![]() t-
t-![]() =0,|PA|·|PB|=|t1t2|=
=0,|PA|·|PB|=|t1t2|=![]() .故点P到点A、B两点的距离之积为
.故点P到点A、B两点的距离之积为![]() .
.
试题解析:(1)直线l的参数方程为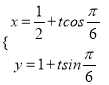 ,即
,即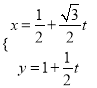 (t为参数)
(t为参数)
由![]() ,得ρ=cosθ+sinθ,所以ρ2=ρcosθ+ρsinθ,
,得ρ=cosθ+sinθ,所以ρ2=ρcosθ+ρsinθ,
∵ρ2=x2+y2,ρcosθ=x,ρsinθ=y,∴![]() .
.
(2)把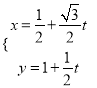 代入
代入![]() .
.
得t2+![]() t-
t-![]() =0,|PA|·|PB|=|t1t2|=
=0,|PA|·|PB|=|t1t2|=![]() .故点P到点A、B两点的距离之积为
.故点P到点A、B两点的距离之积为![]() .
.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ) 当a=-1时,求证: ![]() ;
;
(Ⅱ) 对任意![]() ,存在
,存在![]() ,使
,使![]() 成立,求a的取值范围.
成立,求a的取值范围.
(其中e是自然对数的底数,e=2.71828…)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过椭圆![]() :
: ![]() 的左右焦点
的左右焦点![]() 分别作直线
分别作直线![]() ,
, ![]() 交椭圆于
交椭圆于![]() 与
与![]() ,且
,且![]() .
.
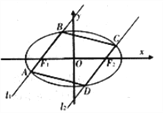
(1)求证:当直线![]() 的斜率
的斜率![]() 与直线
与直线![]() 的斜率
的斜率![]() 都存在时,
都存在时, ![]() 为定值;
为定值;
(2)求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】五边形![]() 是由一个梯形
是由一个梯形![]() 与一个矩形
与一个矩形![]() 组成的,如图甲所示,B为AC的中点,
组成的,如图甲所示,B为AC的中点, ![]() . 先沿着虚线
. 先沿着虚线![]() 将五边形
将五边形![]() 折成直二面角
折成直二面角![]() ,如图乙所示.
,如图乙所示.
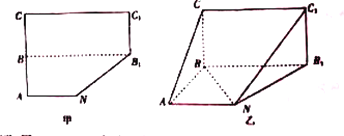
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求图乙中的多面体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且
,且![]() 的图象与直线
的图象与直线![]() 的两个相邻公共点之间的距离为
的两个相邻公共点之间的距离为![]() .
.
(1)求函数![]() 的解析式,并求出
的解析式,并求出![]() 的单调递增区间;
的单调递增区间;
(2)将函数![]() 的图象上所有点向左平移
的图象上所有点向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,设
的图象,设![]() ,
, ![]() ,
, ![]() 为
为![]() 的三个内角,若
的三个内角,若![]() ,且向量
,且向量![]() ,
, ![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,![]() ,
,![]() =4 ,
=4 ,![]() ,F为棱AE的中点.
,F为棱AE的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教师有相同的语文参考书3本,相同的数学参考书4本,从中取出4本赠送给4位学生,每位学生1本,则不同的赠送方法共有( )
A. 15种 B. 20种 C. 48种 D. 60种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com