
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ) 当a=-1时,求证: ![]() ;
;
(Ⅱ) 对任意![]() ,存在
,存在![]() ,使
,使![]() 成立,求a的取值范围.
成立,求a的取值范围.
(其中e是自然对数的底数,e=2.71828…)
【答案】(Ⅰ)详见解析(Ⅱ)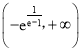
【解析】试题分析:
(1)写出![]() 时的函数解析式,然后由导函数求得原函数的单调性,最后求得最大值:
时的函数解析式,然后由导函数求得原函数的单调性,最后求得最大值: ![]() 即可证得题中的结论;
即可证得题中的结论;
(2)将问题转化为![]() ,利用导函数的相关结论讨论最值得到关于实数
,利用导函数的相关结论讨论最值得到关于实数![]() 的不等式即可求得最终结果.
的不等式即可求得最终结果.
试题解析:
(Ⅰ)当a=-1时, ![]() (x>0),
(x>0),
则![]() ,令
,令![]() ,得
,得![]() .
.
当![]() 时,
时, ![]() ,
, ![]() 单调递增;当
单调递增;当![]() 时,
时, ![]() ,
, ![]() 单调递减.
单调递减.
故当![]() 时,函数
时,函数![]() 取得极大值,也为最大值,所以
取得极大值,也为最大值,所以![]() ,
,
所以, ![]() ,得证.
,得证.
(II)原题即对任意![]() ,存在
,存在![]() ,使
,使![]() 成立,
成立,
只需![]() .
.
设![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() 对于
对于![]() 恒成立,
恒成立,
所以![]() 为
为![]() 上的增函数,
上的增函数,
于是![]() ,即
,即![]() 对于
对于![]() 恒成立,
恒成立,
所以![]() 为
为![]() 上的增函数,则
上的增函数,则![]() .
.
令![]() ,则
,则![]() ,
,
当a≥0时, ![]() 为
为![]() 的减函数,且其值域为R,符合题意.
的减函数,且其值域为R,符合题意.
当a<0时, ![]() ,由
,由![]() 得
得![]() ,
,
由![]() 得
得![]() ,则p(x)在
,则p(x)在![]() 上为增函数;由
上为增函数;由![]() 得
得![]() ,则p(x)在
,则p(x)在![]() 上为减函数,所以
上为减函数,所以![]() ,
,
从而由![]() ,解得
,解得![]() .
.
综上所述,a的取值范围是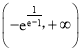 .
.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】祖暅是南北朝时代的伟大科学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖出一个圆锥所得的几何体;图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为( )
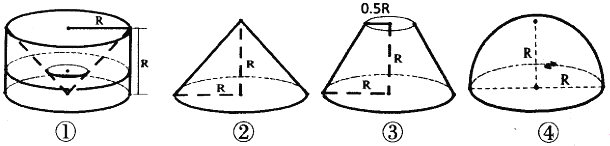
A. ①② B. ①③ C. ②④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:
·(1)y=|cos(2x+ ![]() )|最小正周期为π;
)|最小正周期为π;
·(2)函数y=tan ![]() 的图象的对称中心是(kπ,0),k∈Z;
的图象的对称中心是(kπ,0),k∈Z;
·(3)f(x)=tanx﹣sinx在(﹣ ![]() ,
, ![]() )上有3个零点;
)上有3个零点;
·(4)若 ![]() ∥
∥ ![]() ,
, ![]() ,则
,则 ![]()
其中错误的是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]()
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)令![]() ,其图象上任意一点
,其图象上任意一点![]() 处切线的斜率
处切线的斜率![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)当![]() 时,方程
时,方程![]() 在区间
在区间![]() 内有唯一实数解,求实数
内有唯一实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,海中有一小岛,周围3.8海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.若此舰不改变舰行的方向继续前进,问此舰有没有触礁的危险?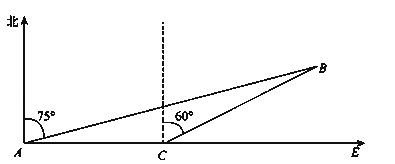
查看答案和解析>>
科目:高中数学 来源: 题型:
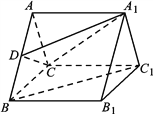
【题目】如图,在三棱柱![]() 中,底面△ABC是等边三角形,侧面
中,底面△ABC是等边三角形,侧面![]() 为正方形,且
为正方形,且![]() 平面ABC,
平面ABC, ![]() 为线段
为线段![]() 上的一点.
上的一点.
(Ⅰ) 若![]() ∥平面A1CD,确定D的位置,并说明理由;
∥平面A1CD,确定D的位置,并说明理由;
(Ⅱ) 在(Ⅰ)的条件下,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校计划面向高一年级![]() 名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了
名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了![]() 名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有
名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有![]() 人.在这
人.在这![]() 名学生中选择社会科学类的男生、女生均为
名学生中选择社会科学类的男生、女生均为![]() 人.
人.
(Ⅰ)分别计算抽取的样本中男生及女生选择社会科学类的频率,并以统计的频率作为概率,估计实际选课中选择社会科学类学生数;
(Ⅱ)根据抽取的![]() 名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过
名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过![]() 的前提下认为科类的选择与性别有关?
的前提下认为科类的选择与性别有关?
选择自然科学类 | 选择社会科学类 | 合计 | |
男生 | |||
女生 | |||
合计 |
附: 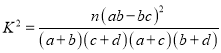 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知直线l经过点![]() ,倾斜角
,倾斜角![]() ,圆
,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出直线l的参数方程,并把圆![]() 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(Ⅱ)设l与圆![]() 相交于
相交于![]() 两点,求点
两点,求点![]() 到
到![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com