Question

【题目】如图所示，在正方体中，E是棱的中点，F是侧面内的动点，且平面，给出下列命题：

点F的轨迹是一条线段；与不可能平行；与BE是异面直线；平面不可能与平面平行．

其中正确的个数是　　

A. 0B. 1C. 2D. 3

Answer 1

【答案】D

【解析】

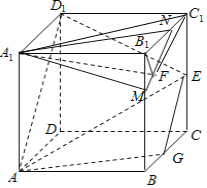
先设平面与直线BC交于点G，连接AG、EG，则G为BC的中点，分别取B、的中点M、N，连接AM、MN、AN，推导出平面平面，即可判断；根据异面直线的概念，即可判断；根据面面位置关系判断.

对于，设平面与直线BC交于点G，连接AG、EG，则G为BC的中点，

分别取B、的中点M、N，连接M、MN、N，，平面，平面，

平面同理可得平面，、MN是平面内的相交直线

平面平面，由此结合平面，可得直线平面，

即点F是线段MN上的动点，正确；

对于，由知，平面平面，当F与点M重合时，，错误；对于，平面平面，BE和平面相交，所以BE不平行平面，又由知：点F是线段MN上的动点，所以与BE不相交，与BE是异面直线，正确；

对于，由与EG相交，可得平面与平面相交，正确．

综上，以上正确的命题是共3个．

故选：D．