
 已知在梯形ABCD中,∠ADC=$\frac{π}{2}$,AB∥CD,PC⊥平面ABCD,CP=AB=2DC=2DA,点E在BP上,且EB=2PE.
已知在梯形ABCD中,∠ADC=$\frac{π}{2}$,AB∥CD,PC⊥平面ABCD,CP=AB=2DC=2DA,点E在BP上,且EB=2PE.分析 (1)连接DB交AC于点O,连接OE,由已知结合平行线成比例可得OE∥PD.再由线面平行的判定可得DP∥平面ACE;
(2)设CD=1,由∠ADC=$\frac{π}{2}$,且PC⊥平面ABCD,故以C为原点,过点C与AD平行的直线为x轴,CD所在直线为y轴,CP所在直线为z轴距离空间直角坐标系.求出平面ACE的一个法向量,再证明MD⊥平面PAC,可得$\overrightarrow{MD}$是平面PAC的一个法向量.由两法向量所成角的余弦值求得二面角E-AC-P的余弦值.
解答 (1)证明:连接DB交AC于点O,连接OE,
∵AB∥CD,∴$\frac{DO}{OB}=\frac{CD}{AB}=\frac{1}{2}$,
∵EB=2PE,∴$\frac{PE}{EB}=\frac{1}{2}=\frac{DO}{OB}$,
∴OE∥PD.
∵DP?平面ACE,OE?平面ACE,
∴DP∥平面ACE;
(2)解:设CD=1,∵∠ADC=$\frac{π}{2}$,且PC⊥平面ABCD,
故以C为原点,过点C与AD平行的直线为x轴,CD所在直线为y轴,CP所在直线为z轴距离空间直角坐标系.
则C(0,0,0),A(1,1,0),B(1,-1,0),D(0,1,0),P(0,0,2),
设E(xE,yE,zE),由EB=2PE,得$\overrightarrow{PE}=\frac{1}{3}\overrightarrow{PB}$,
∴(xE,yE,zE-2)=$\frac{1}{3}$(1,-1,-2),得E($\frac{1}{3},-\frac{1}{3},\frac{4}{3}$).
$\overrightarrow{CA}=(1,1,0),\overrightarrow{CE}=(\frac{1}{3},-\frac{1}{3},\frac{4}{3})$,
设平面ACE的一个法向量为$\overrightarrow{n}=(x,y,z)$.
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{CA}=x+y=0}\\{\overrightarrow{n}•\overrightarrow{CE}=\frac{1}{3}x-\frac{1}{3}y+\frac{4}{3}z=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}=(1,-1,-\frac{1}{2})$.
取AC的中点M,连接MD,可得M($\frac{1}{2},\frac{1}{2},0$),
∴$\overrightarrow{MD}=(-\frac{1}{2},\frac{1}{2},0)$.
由DA=DC,得MD⊥AC,
由PC⊥底面ABCD,得MD⊥PC,
又AC∩PC=C,∴MD⊥平面PAC,
∴$\overrightarrow{MD}$是平面PAC的一个法向量.
∴|cos<$\overrightarrow{MD},\overrightarrow{n}$>|=$\frac{|\overrightarrow{MD}•\overrightarrow{n}|}{|\overrightarrow{MD}|•|\overrightarrow{n}|}=\frac{|-\frac{1}{2}-\frac{1}{2}|}{\frac{\sqrt{2}}{2}•\sqrt{2+\frac{1}{4}}}=\frac{2\sqrt{2}}{3}$.
由图可知,二面角E-AC-P为锐二面角,
∴二面角E-AC-P的余弦值为$\frac{2\sqrt{2}}{3}$.
点评 本题考查直线与平面平行的判定,考查空间想象能力和思维能力,训练了利用空间向量求二面角的大小,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
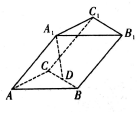 如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的等边三角形,点A1在底面ABC上的投影D恰好为BC的中点,AA1与平面ABC所成角为45°,则该三棱柱的体积为( )
如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的等边三角形,点A1在底面ABC上的投影D恰好为BC的中点,AA1与平面ABC所成角为45°,则该三棱柱的体积为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某学校为了加强学生的安全教育,对学校旁边A,B两个路口进行了8天的监测调查,得到每天路口不按交通规则过马路的学生人数(如茎叶图所示),且A路口数据的平均数比B路口数据的平均数小2.
某学校为了加强学生的安全教育,对学校旁边A,B两个路口进行了8天的监测调查,得到每天路口不按交通规则过马路的学生人数(如茎叶图所示),且A路口数据的平均数比B路口数据的平均数小2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3+$\sqrt{2}$ | B. | $\sqrt{10}$+$\sqrt{2}$ | C. | $\sqrt{5}$+$\sqrt{2}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com