
【题目】已知函数f(x)=|x﹣a|+|x+1|(a∈R),g(x)=|2x﹣1|+2.
(1)若a=1,证明:不等式f(x)≤g(x)对任意的x∈R成立;
(2)若对任意的m∈R,都有t∈R,使得f(m)=g(t)成立,求实数a的取值范围.
【答案】(1)证明见解析;(2)a≤﹣3或a≥1.
【解析】
(1)a=1时函数![]() ,利用分段讨论法比较f(x)与g(x)的大小即可;
,利用分段讨论法比较f(x)与g(x)的大小即可;
(2)由题意知f(x)的值域包含于g(x)的值域,分别求出f(x)、g(x)的值域,列出不等式求得a的取值范围.
(1)a=1时,函数f(x)=|x﹣1|+|x+1|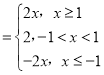 ,
,
g(x)=|2x﹣1|+2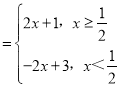 ;
;
①当x≥1时,2x<2x+1,即f(x)<g(x);
②当![]() x<1时,2≤2x+1,即
x<1时,2≤2x+1,即![]() ;
;
③当﹣1<x![]() 时,2<﹣2x+3,即f(x)<g(x);
时,2<﹣2x+3,即f(x)<g(x);
④当x≤﹣1时,﹣2x<﹣2x+3,即f(x)<g(x);
综上知,a=1时,不等式f(x)≤g(x)对任意的x∈R成立;
(2)对任意的m∈R,都有t∈R,使得f(m)=g(t)成立,
所以f(x)的值域包含于g(x)的值域;
由f(x)=|x﹣a|+|x+1|≥|(x﹣a)﹣(x+1)|=|a+1|,
所以f(x)的值域为[|a+1|,+∞);
又g(x)=|2x﹣1|+2≥2,
所以g(x)的值域为[2,+∞);
所以|a+1|≥2,即a+1≥2或a+1≤﹣2,解得a≥1或a≤﹣3;
所以实数a的取值范围是a≤﹣3或a≥1.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】已知点P(1,2)在抛物线C:y2=2px(p>0)上.
(Ⅰ)求C的方程;
(Ⅱ)斜率为﹣1的直线与C交于异于点P的两个不同的点M,N,若直线PM,PN分别与x轴交于A,B两点,求证:△PAB为等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求实数
垂直,求实数![]() 的值;
的值;
(Ⅱ)求函数![]() 的单调区间;
的单调区间;
(Ⅲ)用![]() 表示
表示![]() ,
,![]() 中的较大者,记函数
中的较大者,记函数![]() .若函数
.若函数![]() 在
在![]() 内恰有2个零点,求实数
内恰有2个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() l(a>b>0)经过点(
l(a>b>0)经过点(![]() ,1),且离心率e
,1),且离心率e![]() .
.
(1)求椭圆C的方程;
(2)若直线l与椭圆C相交于AB两点,且满足∠AOB=90°(O为坐标原点),求|AB|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)求购买金额不少于45元的频率;
(2)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
女 | 18 | ||
合计 |
附:参考公式和数据: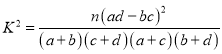 ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() 满足
满足![]() ,且
,且![]() .正项数列
.正项数列![]() 满足
满足![]() ,其前7项和为42.
,其前7项和为42.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意正整数
,若对任意正整数![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)将数列![]() ,
,![]() 的项按照“当
的项按照“当![]() 为奇数时,
为奇数时,![]() 放在前面;当
放在前面;当![]() 为偶数时,
为偶数时,![]() 放在前面”的要求进行排列,得到一个新的数列:
放在前面”的要求进行排列,得到一个新的数列:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,求这个新数列的前
,…,求这个新数列的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,![]() 在线段
在线段![]() 上,且
上,且![]() 。将
。将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到
到![]() 的位置(如图2所示),且
的位置(如图2所示),且![]() 。
。
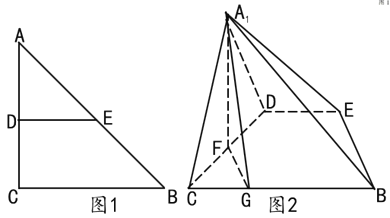
(1)证明:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值
所成锐二面角的余弦值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com