
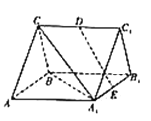
【题目】如图,在直三棱柱![]() 中,
中,![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点.
的中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见证明;(2) ![]()
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,据题设可得四边形
,据题设可得四边形![]() 是平行四边形,根据线面平行的证明定理即可得证;
是平行四边形,根据线面平行的证明定理即可得证;
(2)延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,根据题设条件可证明
,根据题设条件可证明![]() ,
,![]() ,
,![]() 两两垂直,因而以O为原点,以
两两垂直,因而以O为原点,以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向建立空间直角坐标系,写出各个点的坐标,即可求得平面
轴的正方向建立空间直角坐标系,写出各个点的坐标,即可求得平面![]() 的法向量为,根据直线与平面夹角的正弦值为直线与平面法向量夹角的余弦值即可得解
的法向量为,根据直线与平面夹角的正弦值为直线与平面法向量夹角的余弦值即可得解
(1)证明:设点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() ,
,
∵![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴![]() ,且
,且![]() .
.
又在平行四边形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,
∴![]() ,且
,且![]() ,
,
∴![]() ,且
,且![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() .
.
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)解:如图,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
则由(1)![]() 及
及![]() 知
知![]() ,
,
且![]() 是
是![]() 的中点,
的中点,
∵![]() 是正三角形,
是正三角形,
∴![]() .
.
又在直三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,故
,故![]() ,
,
所以![]() ,
,![]() ,
,![]() 两两垂直.
两两垂直.
如图,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系![]() ,
,
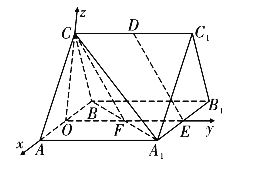
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则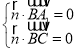 ,即
,即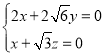 ,解得
,解得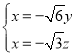 ,
,
∴可取![]() .
.
设直线![]() 与平面
与平面![]() 的所成角为
的所成角为![]() ,
,
则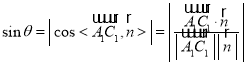
![]() ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】农机公司出售收割机,一台收割机的使用寿命为五年,在农机公司购买收割机时可以一次性额外订购买若干次维修服务,费用为每次100元,每次维修时公司维修人员均上门服务,实际上门服务时还需支付维修人员的餐饮费50元/次;若实际维修次数少于购买的维修次数,则未提供服务的订购费用退还50%;如果维修次数超过了购买的次数,农机公司不再提供服务,收割机的维修只能到私人维修店,每次维修费用为400元,无须支付餐饮费;--位农机手在购买收割机时,需决策一次性购买多少次维修服务.
为此,他拟范收集整理出一台收割机在五年使用期内维修次数及相应的频率如下表:

(1)如果农机手在购买收割机时购买了6次维修,在使用期内实际维修的次数为5次,这位农机手的花费总费用是多少?如果实际维修的次数是8次,农机手的花费总费用又是多少?
(2)农机手购买了一台收制机,试在购买维修次数为6次和7次的两个数据中,根据使用期内维修时花费的总费用期望值,帮助农机手进行决策.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图像向右平移
的图像向右平移![]() 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的![]() 倍(纵坐标不变)得到函数
倍(纵坐标不变)得到函数![]() 的图像,则下列说法正确的是( )
的图像,则下列说法正确的是( )
A. 函数![]() 的最小正周期为
的最小正周期为![]()
B. 函数![]() 在区间
在区间![]() 上单调递增
上单调递增
C. 函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]()
D. ![]() 是函数
是函数![]() 的一条对称轴
的一条对称轴
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 前n项和为
前n项和为![]() ,且
,且![]() 其中m为实常数,
其中m为实常数,![]() 且
且![]() .
.
(1)求证:![]() 是等比数列;
是等比数列;
(2)若数列![]() 的公比满足
的公比满足![]() 且
且![]() ,
,![]() ,求证:数列
,求证:数列![]() 是等差数列,并求
是等差数列,并求![]() 的通项公式;
的通项公式;
(3)若![]() 时,设
时,设![]() ,求数列
,求数列![]() 的前n和
的前n和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论:
①在回归分析模型中,残差平方和越大,说明模型的拟合效果越好;
②某学校有男教师60名、女教师40名,为了解教师的体育爱好情况,在全体教师中抽取20名调查,则宜采用的抽样方法是分层抽样;
③线性相关系数![]() 越大,两个变量的线性相关性越弱;反之,线性相关性越强;
越大,两个变量的线性相关性越弱;反之,线性相关性越强;
④在回归方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 增加0.5个单位.
增加0.5个单位.
其中正确的结论是( )
A. ①②B. ①④
C. ②③D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D1中,点O是四边形ABCD的中心,关于直线A1O,下列说法正确的是( )
A. A1O∥DCB. A1O⊥BCC. A1O∥平面BCDD. A1O⊥平面ABD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com