
【题目】已知椭圆![]() 的离心率
的离心率![]() ,椭圆
,椭圆![]() 上的点到其左焦点
上的点到其左焦点![]() 的最大距离为
的最大距离为![]() .
.
(1)求椭圆的标准方程;
(2)过椭圆![]() 左焦点
左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线与直线
的垂线与直线![]() 交于点
交于点![]() ,求
,求![]() 的最小值和此时直线
的最小值和此时直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)最小值为
;(2)最小值为![]() ,此时直线
,此时直线![]() 的方程为
的方程为![]() .
.
【解析】
(1)根据椭圆![]() 上的点到其左焦点的最大距离为
上的点到其左焦点的最大距离为![]() ,得到
,得到![]() ,再由
,再由![]() ,联立求解即可.
,联立求解即可.
(2)①当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() ,可分别求导T,A,B的坐标,然后利用两点间距离公式求解;②当直线
,可分别求导T,A,B的坐标,然后利用两点间距离公式求解;②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,由
,由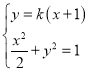 ,利用弦长公式求得
,利用弦长公式求得![]() ,再由
,再由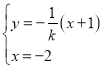 ,求得交点
,求得交点![]() ,从而得到
,从而得到![]() ,代入
,代入![]() 求解.
求解.
(1)由题可知![]() ,又椭圆
,又椭圆![]() 上的点到其左焦点的最大距离为
上的点到其左焦点的最大距离为![]() ,
,
所以![]() ,
,
所以![]() ,
,![]() ,
,
∴![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)①当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() ,则
,则![]() ,
,
所以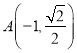 ,
,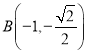 ,此时
,此时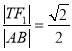 ;
;
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]()
由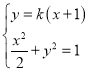 ,
,
得![]() ,
,
由韦达定理得![]() ,
,![]() ,
,
则![]() ,
,
联立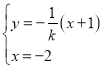 ,可得
,可得![]() ,
,
所以![]()
所以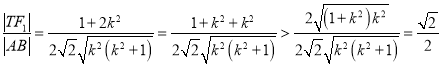 .
.
因为![]() 所以等号不成立.
所以等号不成立.
综上,![]() 的最小值为
的最小值为![]() ,此时直线
,此时直线![]() 的方程为
的方程为![]() .
.


 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
【题目】“杂交水稻之父”袁隆平一生致力于杂交水稻技术的研究、应用与推广,发明了“三系法”籼型杂交水稻,成功研究出“两系法”杂交水稻,创建了超级杂交稻技术体系,为我国粮食安全、农业科学发展和世界粮食供给做出了杰出贡献;某杂交水稻种植研究所调查某地水稻的株高,得出株高(单位:cm)服从正态分布,其密度曲线函数为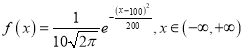 ,则下列说法正确的是( )
,则下列说法正确的是( )
A.该地水稻的平均株高为100cm
B.该地水稻株高的方差为10
C.随机测量一株水稻,其株高在120cm以上的概率比株高在70cm以下的概率大
D.随机测量一株水稻,其株高在(80,90)和在(100,110)(单位:cm)的概率一样大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】湖北七市州高三5月23日联考后,从全体考生中随机抽取44名,获取他们本次考试的数学成绩![]() 和物理成绩
和物理成绩![]() ,绘制成如图散点图:
,绘制成如图散点图:
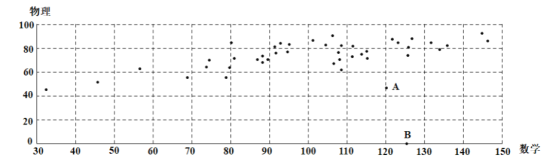
根据散点图可以看出![]() 与
与![]() 之间有线性相关关系,但图中有两个异常点
之间有线性相关关系,但图中有两个异常点![]() .经调查得知,
.经调查得知,![]() 考生由于重感冒导致物理考试发挥失常,
考生由于重感冒导致物理考试发挥失常,![]() 考生因故未能参加物理考试.为了使分析结果更科学准确,剔除这两组数据后,对剩下的数据作处理,得到一些统计的值:
考生因故未能参加物理考试.为了使分析结果更科学准确,剔除这两组数据后,对剩下的数据作处理,得到一些统计的值:![]()
![]()
![]() 其中
其中![]() ,
,![]() 分别表示这42名同学的数学成绩、物理成绩,
分别表示这42名同学的数学成绩、物理成绩,![]() ,2,…,42,
,2,…,42,![]() 与
与![]() 的相关系数
的相关系数![]() .
.
(1)若不剔除![]() 两名考生的数据,用44组数据作回归分析,设此时
两名考生的数据,用44组数据作回归分析,设此时![]() 与
与![]() 的相关系数为
的相关系数为![]() .试判断
.试判断![]() 与
与![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
(2)求![]() 关于
关于![]() 的线性回归方程,并估计如果
的线性回归方程,并估计如果![]() 考生参加了这次物理考试(已知
考生参加了这次物理考试(已知![]() 考生的数学成绩为125分),物理成绩是多少?
考生的数学成绩为125分),物理成绩是多少?
(3)从概率统计规律看,本次考试七市州的物理成绩![]() 服从正态分布
服从正态分布![]() ,以剔除后的物理成绩作为样本,用样本平均数
,以剔除后的物理成绩作为样本,用样本平均数![]() 作为
作为![]() 的估计值,用样本方差
的估计值,用样本方差![]() 作为
作为![]() 的估计值.试求七市州共50000名考生中,物理成绩位于区间(62.8,85.2)的人数
的估计值.试求七市州共50000名考生中,物理成绩位于区间(62.8,85.2)的人数![]() 的数学期望.
的数学期望.
附:①回归方程![]() 中:
中: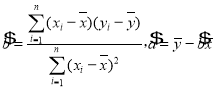
②若![]() ,则
,则![]()
③![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点
的焦点![]() 到准线
到准线![]() 的距离为2,直线
的距离为2,直线![]() 与抛物线交于不同的两点
与抛物线交于不同的两点![]() ,
,![]() .
.
(1)求抛物线的方程;
(2)是否存在与![]() 的取值无关的定点
的取值无关的定点![]() ,使得直线
,使得直线![]() ,
,![]() 的斜率之和恒为定值?若存在,求出所有点
的斜率之和恒为定值?若存在,求出所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题共l4分)
已知函数f(x)=![]() x +
x +![]() , h(x)=
, h(x)=![]() .
.
(I)设函数F(x)=f(x)一h(x),求F(x)的单调区间与极值;
(Ⅱ)设a∈R,解关于x的方程log4[![]() ]=1og2h(a-x)一log2h (4-x);
]=1og2h(a-x)一log2h (4-x);
(Ⅲ)试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《算法统宗》是中国古代数学名著,由明代数学家程大位编著,它对我国民间普及珠算和数学知识起到了很大的作用,是东方古代数学的名著.在这部著作中,许多数学问题都是以歌诀形式呈现的,“九儿问甲歌”就是其中一首:“一个公公九个儿,若问生年总不知,自长排来差三岁,共年二百又零七,借问长儿多少岁,各儿岁数要详推.”这首歌决的大意是:“一位老公公有九个儿子,九个儿子从大到小排列,相邻两人的年龄差三岁,并且儿子们的年龄之和为207岁,请问大儿子多少岁,其他几个儿子年龄如何推算.”在这个问题中,记这位公公的第![]() 个儿子的年龄为
个儿子的年龄为![]() ,则
,则![]() ( )
( )
A.17B.29C.23D.35
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以坐标原点O为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为:
轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为:![]() ,曲线C2的参数方程为:
,曲线C2的参数方程为: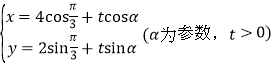 ,点N的极坐标为
,点N的极坐标为![]() .
.
(Ⅰ)若M是曲线C1上的动点,求M到定点N的距离的最小值;
(Ⅱ)若曲线C1与曲线C2有有两个不同交点,求正数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的奇函数![]() ,满足
,满足 ,则下列叙述正确的为( )
,则下列叙述正确的为( )
①存在实数k,使关于x的方程![]() 有7个不相等的实数根
有7个不相等的实数根
②当![]() 时,恒有
时,恒有![]()
③若当![]() 时,
时,![]() 的最小值为1,则
的最小值为1,则![]()
④若关于![]() 的方程
的方程![]() 和
和![]() 的所有实数根之和为零,则
的所有实数根之和为零,则![]()
A.①②③B.①③C.②④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com