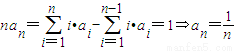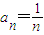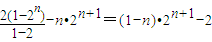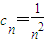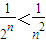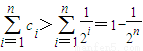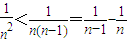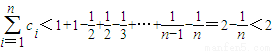【答案】
分析:(Ⅰ)已知S
n求a
n的问题可以利用
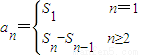
进行求解,能合并就合并,从而求出数列{a
n}的通项公式;
(Ⅱ)根据(Ⅰ)求得 b
n=n•2
n,是由一个等差数列与一等比数列的乘积,可利用错位相减法进行求和,再S
n的等式两边同时乘以公比,然后进行作差即可求出数列{b
n}的前n项和S
n;
(III))把(Ⅰ)求得的结果代入,通过对c
n进行放缩,达到求和的目的,从而证明了不等式的右边;要证不等式的左边,构造函数f(x)=2
x-x
2,求导,借助于该函数的单调性证明该不等式的左边,从而证明结论正确.
解答:解:(I)当n≥2时,
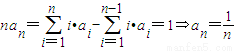
当n=1时,a
1=1成立,故
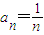
(II)b
n=n•2
n
S
n=1•2
1+2•2
2+3•2
3+…+n•2
n①
2S
n=1•2
2+2•2
3+3•2
4+…+(n-1)•2
n+n•2
n+1②
由①-②得,-S
n=2
1+2
2+2
3++2
n-n•2
n+1
=
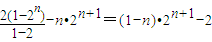
故S
n=(n-1)•2
n+1+2
(III)证明:
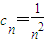
令f(x)=2
x-x
2
f′(x)=2
xln2-2x,又

故f′′(x)=2
x(ln2)
2-2≥f′′(5)>0
故f′(x)在[5,+∞)上单调递增,故f′(x)≥f′(5)>0
故f(x)在[5,+∞)上单调递增,故f(x)≥f(5)=7>0
故当n>4时,2
n>n
2恒成立,即
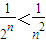
故
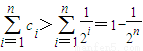
又
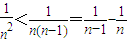
故
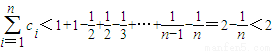
综上可得,
 点评:
点评:此题是难题.考查学生根据数列递推公式求数列的通项公式并利用错位相减法求和,以及把不能求和的数列问题通过放缩的方法达到求和的目的.特别是问题(III)的设问形式,构造函数,借助于函数的单调性证明数列不等式,是高考的热点,也是难点,注意体会.

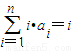 .
.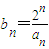 ,求bn的前n项和Sn;
,求bn的前n项和Sn;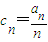 .求证:
.求证: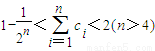 .
.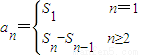 进行求解,能合并就合并,从而求出数列{an}的通项公式;
进行求解,能合并就合并,从而求出数列{an}的通项公式;