
【题目】已知函数f(x)=loga(x+1),g(x)=2loga(2x+t)(t∈R),a>0,且a≠1. (Ⅰ)若3是关于x的方程f(x)﹣g(x)=0的一个解,求t的值;
(Ⅱ)当0<a<1且t=1时,解不等式f(x)≤g(x);
(Ⅲ)若函数F(x)=af(x)+tx2﹣2t+1在区间(﹣1,3]上有零点,求t的取值范围.
【答案】解:(Ⅰ)∵3是关于x的方程f(x)﹣g(x)=0的一个解, ∴loga4﹣2loga(6+t)=0,
∴2=(2+t)2 ,
∴t=﹣4.
(Ⅱ)当0<a<1且t=1时,不等式f(x)≤g(x)化为  ,∴﹣
,∴﹣ ![]()
∴解集为:{x|﹣ ![]() };
};
(Ⅲ)F(x)=af(x)+tx2﹣2t+1
=x+1+tx2﹣2t+1=tx2+x﹣2t+2,
令tx2+x﹣2t+2=0,
即t(x2﹣2)=﹣(x+2),
∵x∈(﹣1,3],∴x+2∈(1,5],
∴t≠0,x2﹣2≠0;
∴ ![]() =﹣[(x+2)+
=﹣[(x+2)+ ![]() ]+4,
]+4,
∵2 ![]() ≤(x+2)+
≤(x+2)+ ![]() ≤
≤ ![]() ,
,
∴﹣ ![]() ≤﹣[(x+2)+
≤﹣[(x+2)+ ![]() ]+4≤4﹣2
]+4≤4﹣2 ![]() ,
,
∴t≤﹣ ![]() 或t≥
或t≥ ![]() .
.
【解析】(Ⅰ)由题意得loga4﹣2loga(6+t)=0,从而解得t的值;(Ⅱ)由题意得loga(x+1)≤2loga(2x+1),由对数函数的单调性可得,从而得 ![]() 解.(Ⅲ)化简F(x)=tx2+x﹣2t+2,从而令tx2+x﹣2t+2=0,讨论可得
解.(Ⅲ)化简F(x)=tx2+x﹣2t+2,从而令tx2+x﹣2t+2=0,讨论可得 ![]() =﹣[(x+2)+
=﹣[(x+2)+ ![]() ]+4,从而得解.
]+4,从而得解.


科目:高中数学 来源: 题型:
【题目】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图,图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃,下面叙述不正确的是( ) 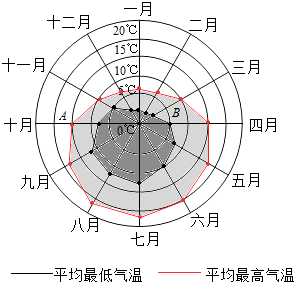
A.各月的平均最低气温都在0℃以上
B.七月的平均温差比一月的平均温差大
C.三月和十一月的平均最高气温基本相同
D.平均最高气温高于20℃的月份有5个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50m到达B处,又测得∠DBC=45°,根据以上数据可得cosθ= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足 ![]() =1,公差d∈(﹣1,0),当且仅当n=9时,数列{an}的前n项和Sn取得最大值,则该数列首项a1的取值范围是( )
=1,公差d∈(﹣1,0),当且仅当n=9时,数列{an}的前n项和Sn取得最大值,则该数列首项a1的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.[ ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() )
)
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和Sn , 且a3=7,S11=143, (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=2 ![]() +2n,求数列{bn}的前n项和Tn .
+2n,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x﹣y﹣5=0,AC边上的高BH所在直线方程为x﹣2y﹣5=0.求:
(1)顶点C的坐标;
(2)直线BC的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若△ABC的内角A,B,C的对边分别为a,b,c,已知c=2,C= ![]() .
.
(1)若b= ![]() ,求角B;
,求角B;
(2)若sinC+sin(B﹣A)=2sin2A,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列不等式中正确的是( )
A.sin ![]() π>sin
π>sin ![]() π
π
B.tan ![]() π>tan(﹣
π>tan(﹣ ![]() )
)
C.sin(﹣ ![]() )>sin(﹣
)>sin(﹣ ![]() )
)
D.cos(﹣ ![]() π)>cos(﹣
π)>cos(﹣ ![]() π)
π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com