
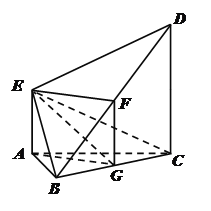
【题目】如图,△![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() 平面
平面![]() ,
,![]() ∥
∥![]() ,
,![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求![]() 点到平面
点到平面![]() 的距离.
的距离.
【答案】(1)证明见解析.
(2)![]()
【解析】分析:(1)先取![]() 边的中点
边的中点![]() ,
,![]() 的中点为
的中点为![]() ,根据三角形中位线性质得四边形
,根据三角形中位线性质得四边形![]() 为平行四边形,即得
为平行四边形,即得![]() ∥
∥![]() .再根据正三角形性质得
.再根据正三角形性质得![]()
![]() ,即得
,即得![]()
![]() .又根据
.又根据![]() 平面
平面![]() ,
,![]() ∥
∥![]() ,易得
,易得![]()
![]() , 即得
, 即得![]()
![]() .由线面垂直判定定理得
.由线面垂直判定定理得![]() 平面
平面![]() ,最后根据面面垂直判定定理得结论,(2)先求三棱锥
,最后根据面面垂直判定定理得结论,(2)先求三棱锥![]() 体积,再根据等体积法求
体积,再根据等体积法求![]() 点到平面
点到平面![]() 的距离.
的距离.
详解:(1)取![]() 边的中点
边的中点![]() ,
,![]() 的中点为
的中点为![]() ,
,
连接![]() ,
,![]() ,
,![]() ,则
,则![]()
![]() .
.
因为![]() 是△
是△![]() 的中位线,由题设
的中位线,由题设
![]() ∥
∥![]() ,且
,且![]() ,所以四边形
,所以四边形![]() 为平行四边形,于是
为平行四边形,于是![]() ∥
∥![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]()
![]() ,
,
所以![]()
![]() ,故
,故![]() 平面
平面![]() .
.
所以![]() 平面
平面![]() ,又
,又![]() 面
面![]() ,
,
故平面![]() 平面
平面![]() .
.
(2)由(1)![]() ,△
,△![]() 面积为2,所以三棱锥
面积为2,所以三棱锥![]() 的体积为
的体积为![]() .
.
由(1)![]() ,
,![]() ,△
,△![]() 面积为2.
面积为2.
设![]() 点到平面
点到平面![]() 的距离为
的距离为![]() ,则三棱锥
,则三棱锥![]() 的体积为
的体积为![]() .
.
因为三棱锥![]() 与三棱锥
与三棱锥![]() 的体积相等,所以
的体积相等,所以![]() ,即
,即![]() 点到平面
点到平面![]() 的距离为
的距离为![]() .
.


科目:高中数学 来源: 题型:
【题目】为了研究家用轿车在高速公路上的车速情况,交通部门随机对50名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况.在30名男性驾驶员中,平均车速超过100![]() 额有20人,不超过100
额有20人,不超过100 ![]() 的有10人;在20名女性驾驶员中,平均车速超过100
的有10人;在20名女性驾驶员中,平均车速超过100![]() 的有5人,不超过100
的有5人,不超过100![]() 的有15人.
的有15人.
(1)完成下面的列联表:
平均车速超过100 | 平均车速不超过100 | 合计 | |
男性驾驶员人数 | |||
女性驾驶员人数 | |||
合计 |
(2)判断是否有99.5%的把握认为,平均车速超过100![]() 与性别有关.
与性别有关.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅是南北朝时代的伟大科学家,公元五世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积恒相等,那么这两个几何体的体积一定相等.设A,B为两个同高的几何体,![]() A,B的体积不相等,
A,B的体积不相等,![]() A,B在等高处的截面积不恒相等.根据祖暅原理可知,p是q的( )
A,B在等高处的截面积不恒相等.根据祖暅原理可知,p是q的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=4cos(ωx﹣ ![]() )sinωx﹣cos(2ωx+π),其中ω>0.
)sinωx﹣cos(2ωx+π),其中ω>0.
(1)求函数y=f(x)的值域
(2)若f(x)在区间 ![]() 上为增函数,求ω的最大值.
上为增函数,求ω的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
极坐标系与直角坐标系![]() 有相同的长度单位,以原点
有相同的长度单位,以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴.曲线
轴正半轴为极轴.曲线![]() 的极坐标方程为
的极坐标方程为![]() ,已知倾斜角为
,已知倾斜角为![]() 的直线
的直线![]() 经过点
经过点![]() .
.
(1)写出直线![]() 的参数方程;曲线
的参数方程;曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 满足
满足![]() .当
.当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,则f(1)+f(2)+…+f(2015)=( )
,则f(1)+f(2)+…+f(2015)=( )
A. 333 B. 336 C. 1678 D. 2015
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为 (t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=2
(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=2![]() sin θ.
sin θ.
(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于点A、B,若点P的坐标为(3,![]() ),求|PA|+|PB|.
),求|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)已知![]() ,记
,记![]() (
(![]() 且
且![]() ),是否存在这样的常数
),是否存在这样的常数![]() ,使得数列
,使得数列![]() 是常数列,若存在,求出
是常数列,若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)若数列![]() ,对于任意的正整数
,对于任意的正整数![]() ,均有
,均有 成立,求证:数列
成立,求证:数列![]() 是等差数列.
是等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com