
【题目】将函数f(x)=cos2x图象向左平移φ(0<φ< ![]() )个单位后得到函数g(x)的图象,若函数g(x)在区间[﹣
)个单位后得到函数g(x)的图象,若函数g(x)在区间[﹣ ![]() ,
, ![]() ]上单调递减,且函数g(x)的最大负零点在区间(﹣
]上单调递减,且函数g(x)的最大负零点在区间(﹣ ![]() ,0)上,则φ的取值范围是( )
,0)上,则φ的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() )
)
 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin(2x+
sin(2x+ ![]() )+sin2x.
)+sin2x.
(1)求函数f(x)的最小正周期;
(2)若函数g(x)对任意x∈R,有g(x)=f(x+ ![]() ),求函数g(x)在[﹣
),求函数g(x)在[﹣ ![]() ,
, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体是由棱台ABC﹣A1B1C1和棱锥D﹣AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2. 
(Ⅰ)求证:平面AB1C⊥平面BB1D;
(Ⅱ)求二面角A1﹣BD﹣C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的方程是y=8,圆C的参数方程是 ![]() (φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求直线l和圆C的极坐标方程;
(2)射线OM:θ=α(其中 ![]() )与圆C交于O、P两点,与直线l交于点M,射线ON:
)与圆C交于O、P两点,与直线l交于点M,射线ON: ![]() 与圆C交于O、Q两点,与直线l交于点N,求
与圆C交于O、Q两点,与直线l交于点N,求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (a∈R),曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直. (Ⅰ)试比较20162017与20172016的大小,并说明理由;
(a∈R),曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直. (Ⅰ)试比较20162017与20172016的大小,并说明理由;
(Ⅱ)若函数g(x)=f(x)﹣k有两个不同的零点x1 , x2 , 证明:x1x2>e2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某重点中学为了解高一年级学生身体发育情况,对全校700名高一年级学生按性别进行分层抽样检查,测得身高(单位:cm)频数分布表如表1、表2. 表1:男生身高频数分布表
身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190) |
频数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2:女生身高频数分布表
身高(cm) | [150,155) | [155,160) | [160,165) | [165,170) | [170,175) | [175,180) |
频数 | 1 | 7 | 12 | 6 | 3 | 1 |
(1)求该校高一女生的人数;
(2)估计该校学生身高在[165,180)的概率;
(3)以样本频率为概率,现从高一年级的男生和女生中分别选出1人,设X表示身高在[165,180)学生的人数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数,则f(x)=sin(2x+ ![]() )+cos(2x+
)+cos(2x+ ![]() ),则( )
),则( )
A.y=f(x)在(0, ![]() )单调递增,其图象关于直线x=
)单调递增,其图象关于直线x= ![]() 对称
对称
B.y=f(x)在(0, ![]() )单调递增,其图象关于直线x=
)单调递增,其图象关于直线x= ![]() 对称
对称
C.y=f(x)在(0, ![]() )单调递减,其图象关于直线x=
)单调递减,其图象关于直线x= ![]() 对称
对称
D.y=f(x)在(0, ![]() )单调递减,其图象关于直线x=
)单调递减,其图象关于直线x= ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体的三视图如图所示,则这个几何体的表面积为( ) 
A.24+8 ![]() +8
+8 ![]()
B.20+8 ![]() +4
+4 ![]() ??
??
C.20+8 ![]() +4
+4 ![]()
D.20+4 ![]() +4
+4 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b分别为16,20,则输出的a=( ) 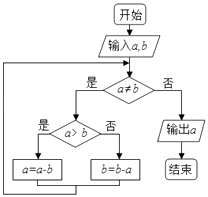
A.0
B.2
C.4
D.14
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com