
【题目】函数y=f(x)与y=g(x)的图象如图所示,则函数y=f(x)g(x)的图象可能是( ) 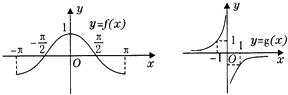
A.
B.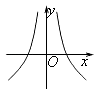
C.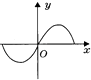
D.
【答案】A
【解析】解:∵y=f(x)的有两个零点,并且g(x)没有零点; ∴函数y=f(x)g(x)也有两个零点M,N,
又∵x=0时,函数值不存在
∴y在x=0的函数值也不存在
当x∈(﹣∞,M)时,y<0;
当x∈(M,0)时,y>0;
当x∈(0,N)时,y<0;
当x∈(N,+∞)时,y>0;
只有A中的图象符合要求
故选:A
本题考查的知识点是函数的图象,由已知中函数y=f(x)与y=g(x)的图象我们不难分析,当函数y=f(x)g(x)有两个零点M,N,我们可以根据函数y=f(x)与y=g(x)的图象中函数值的符号,分别讨论(﹣∞,M)(M,0)(0,N)(N,+∞)四个区间上函数值的符号,以确定函数的图象.


科目:高中数学 来源: 题型:
【题目】设函数y=lg(﹣x2+4x﹣3)的定义域为A,函数y= ![]() ,x∈(0,m)的值域为B.
,x∈(0,m)的值域为B.
(1)当m=2时,求A∩B;
(2)若“x∈A”是“x∈B”的必要不充分条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题: ①若a<b,则a2<b2;
②若a≥b>﹣1,则 ![]() ≥
≥ ![]() ;
;
③若正整数m和n满足m<n,则 ![]() ≤
≤ ![]() ;
;
④若x>0,且x≠1,则lnx+ ![]() ≥2.
≥2.
其中所有真命题的序号是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x3﹣ax﹣b,x∈R,其中a,b∈R. (Ⅰ)求f(x)的单调区间;
(Ⅱ)若f(x)存在极值点x0 , 且f(x1)=f(x0),其中x1≠x0;求证:x1+2x0=0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2019·潍坊期末]某钢铁加工厂新生产一批钢管,为了了解这批产品的质量状况,检验员随机抽取了100件钢管作为样本进行检测,将它们的内径尺寸作为质量指标值,由检测结果得如下频率分布表和频率分布直方图:
分组 | 频数 | 频率 |
25.05~25.15 | 2 | 0.02 |
25.15~25.25 | ||
25.25~25.35 | 18 | |
25.35~25.45 | ||
25.45~25.55 | ||
25.55~25.65 | 10 | 0.1 |
25.65~25.75 | 3 | 0.03 |
合计 | 100 | 1 |

(1)求![]() ,
,![]() ;
;
(2)根据质量标准规定:钢管内径尺寸大于等于25.75或小于25.15为不合格,钢管尺寸在![]() 或
或![]() 为合格等级,钢管尺寸在
为合格等级,钢管尺寸在![]() 为优秀等级,钢管的检测费用为0.5元/根.
为优秀等级,钢管的检测费用为0.5元/根.
(i)若从![]() 和
和![]() 的5件样品中随机抽取2根,求至少有一根钢管为合格的概率;
的5件样品中随机抽取2根,求至少有一根钢管为合格的概率;
(ii)若这批钢管共有2000根,把样本的频率作为这批钢管的频率,有两种销售方案:
①对该批剩余钢管不再进行检测,所有钢管均以45元/根售出;
②对该批剩余钢管一一进行检测,不合格产品不销售,合格等级的钢管50元/根,优等钢管60元/根.
请你为该企业选择最好的销售方案,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆C满足:①截y轴所得弦长为2;②被x轴分成两段圆弧,其弧长的比为3:1,在满足条件①、②的所有圆中,求圆心到直线l:x-2y=0的距离最小的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sin(A﹣B),
=(sin(A﹣B), ![]() ,
, ![]() =(1,2sinB),且
=(1,2sinB),且 ![]()
![]() =﹣sin2C,其中A、B、C分别为△ABC的三边a、b、c所对的角. (Ⅰ)求角C的大小;
=﹣sin2C,其中A、B、C分别为△ABC的三边a、b、c所对的角. (Ⅰ)求角C的大小;
(Ⅱ)若 ![]() ,且S△ABC=
,且S△ABC= ![]() ,求边c的长.
,求边c的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数{an}满a1=0,an+1=an+2n,那a2016的值是( )
A.2014×2015
B.2015×2016
C.2014×2016
D.2015×2015
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1 , 连接AP交棱CC1于点D. (Ⅰ)求证:PB1∥平面BDA1;
(Ⅱ)求二面角A﹣A1D﹣B的平面角的余弦值.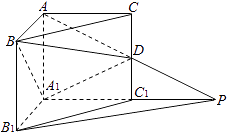
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com