
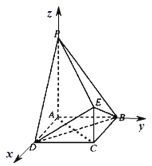
【题目】如图,四边形ABCD为正方形,PA∥CE,AB=CE![]() PA,PA⊥平面ABCD.
PA,PA⊥平面ABCD.
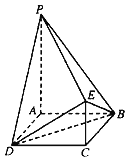
(1)证明:PE⊥平面DBE;
(2)求二面角B﹣PD﹣E的正弦值的大小.
【答案】(1)证明见解析.(2)![]()
【解析】
(1)连结AC,推导出BD⊥AC,PA⊥BD,PA⊥AD,从而BD⊥平面APEC,进而BD⊥PE,推导出PE⊥DE,由此能证明PE⊥平面DBE.
(2)以A为原点,AD,AB,AP所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角B﹣PD﹣E的正弦值.
(1)证明:连结AC,∵四边形ABCD是正方形,
∴BD⊥AC,∵PA⊥平面ABCD,∴PA⊥BD,PA⊥AD,
∵PA∩AC=A,∴BD⊥平面APEC,∵PE平面APEC,
∴BD⊥PE,设AB=1,则AD=1,PA=2,∴PD![]() ,
,
同理解得DE![]() ,在梯形PACE中,解得PE
,在梯形PACE中,解得PE![]() ,
,
∴PE2+DE2=PD2,∴PE⊥DE,∵BD∩DE=D,
∴PE⊥平面DBE.
(2)以A为原点,AD,AB,AP所在直线为x,y,z轴,建立空间直角坐标系,
令AB=1,则CE=1,AP=2,
∴P(0,0,2),E(1,1,1),D(1,0,0),B(0,1,0),
![]() (﹣1,﹣1,1),
(﹣1,﹣1,1),![]() (﹣1,0,2),
(﹣1,0,2),![]() (0,﹣1,2),
(0,﹣1,2),
![]() (1,﹣1,0),设平面DPE的法向量
(1,﹣1,0),设平面DPE的法向量![]() (x,y,z),
(x,y,z),
则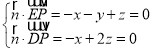 ,取z=1,得
,取z=1,得![]() (2,﹣1,1),
(2,﹣1,1),
设平面BPD的法向量![]() (a,b,c),
(a,b,c),
则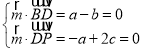 ,取c=1,得
,取c=1,得![]() (2,2,1),
(2,2,1),
设二面角B﹣PD﹣E的平面角为θ,
则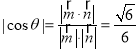 ,
,
∴二面角B﹣PD﹣E的正弦值sinθ![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】国际上通常用年龄中位数指标作为划分国家或地区人口年龄构成的标准:年龄中位数在20岁以下为“年轻型”人口;年龄中位数在20~30岁为“成年型”人口;年龄中位数在30岁以上为“老龄型”人口.

如图反映了我国全面放开二孩政策对我国人口年龄中位数的影响.据此,对我国人口年龄构成的类型做出如下判断:①建国以来直至2000年为“成年型”人口;②从2010年至2020年为“老龄型”人口;③放开二孩政策之后我国仍为“老龄型”人口.其中正确的是( )
A.②③B.①③C.②D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在极坐系中,点![]() 绕极点
绕极点![]() 顺时针旋转角
顺时针旋转角![]() 得到点
得到点![]() .以
.以![]() 为原点,极轴为
为原点,极轴为![]() 轴非负半轴,并取相同的单位长度建立平面直角坐标系,曲线
轴非负半轴,并取相同的单位长度建立平面直角坐标系,曲线![]() 绕
绕![]() 逆时针旋转
逆时针旋转![]() 得到曲线
得到曲线![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 过点
过点![]() 且与曲线
且与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们称满足: ![]() (
(![]() )的数列
)的数列![]() 为“
为“![]() 级梦数列”.
级梦数列”.
(1)若![]() 是“
是“![]() 级梦数列”且
级梦数列”且![]() .求:
.求: ![]() 和
和![]() 的值;
的值;
(2)若![]() 是“
是“![]() 级梦数列”且满足
级梦数列”且满足![]() ,
, ![]() ,求
,求![]() 的最小值;
的最小值;
(3)若![]() 是“0级梦数列”且
是“0级梦数列”且![]() ,设数列
,设数列![]() 的前
的前![]() 项和为
项和为![]() .证明:
.证明: ![]() (
(![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
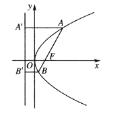
【题目】已知抛物线![]() 为抛物线的焦点,
为抛物线的焦点,![]() 是过焦点的动弦,
是过焦点的动弦,![]() 是
是![]() 两点在准线上的投影,如图所示,则下列论断正确的个数有( )
两点在准线上的投影,如图所示,则下列论断正确的个数有( )
①以![]() 为直径的圆与准线一定相切;
为直径的圆与准线一定相切;
②以![]() 为直径的圆与直线
为直径的圆与直线![]() 一定相切;
一定相切;
③以![]() 为直径的圆与
为直径的圆与![]() 轴一定相切;
轴一定相切;
④以![]() 为直径的圆与
为直径的圆与![]() 轴有可能相切
轴有可能相切
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
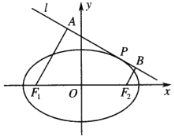
【题目】已知椭圆![]() (
(![]() 为常数且
为常数且![]() )与直线
)与直线![]() 有且只有一个公共点
有且只有一个公共点![]() ,
,![]() .
.
(Ⅰ)当点![]() 的坐标为
的坐标为![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(Ⅱ)过椭圆![]() 的两焦点
的两焦点![]() ,
,![]() 作直线
作直线![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,
,![]() ,求四边形
,求四边形![]() 面积的最大值(用
面积的最大值(用![]() 表示).
表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com