
ΓΨΧβΡΩΓΩΡ≥―ß–Θ‘ΎΤΫΟφΆΦΈΣΨΊ–ΈΒΡ≤Ό≥ΓABCDΡΎΫχ––Χε≤Ό±μ―ίΘ§Τδ÷–ABΘΫ40Θ§BCΘΫ15Θ§OΈΣAB…œ“ΜΒψΘ§«“BOΘΫ10Θ§œΏΕΈOCΓΔODΓΔMNΈΣ±μ―ίΕ”Ν–Υυ‘ΎΈΜ÷ΟΘ®MΓΔNΖ÷±π‘ΎœΏΕΈODΓΔOC…œΘ©Θ§ΓςOCDΡΎΒΡΒψPΈΣΝλΕ”ΈΜ÷ΟΘ§«“PΒΫOCΓΔODΒΡΨύάκΖ÷±πΈΣ![]() ΓΔ
ΓΔ![]() Θ§Φ«OMΘΫdΘ§Έ“Ο«÷ΣΒάΒ±ΓςOMNΟφΜΐΉν–Γ ±Ιέ…Ά–ßΙϊΉνΚΟΘ°
Θ§Φ«OMΘΫdΘ§Έ“Ο«÷ΣΒάΒ±ΓςOMNΟφΜΐΉν–Γ ±Ιέ…Ά–ßΙϊΉνΚΟΘ°
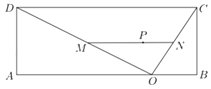
Θ®1Θ©Β±dΈΣΚΈ÷Β ±Θ§PΈΣΕ”Ν–MNΒΡ÷–ΒψΘΜ
Θ®2Θ©‘θ―υΑ≤≈≈MΒΡΈΜ÷Ο≤≈Ρή ΙΙέ…Ά–ßΙϊΉνΚΟΘΩ«σ≥ω¥Υ ±ΓςOMNΒΡΟφΜΐΘ°
ΓΨ¥πΑΗΓΩ(1)![]() Θ°(2) MΘ§NΘ§P »ΐΒψΙ≤œΏΘ§ΟφΜΐΈΣ
Θ°(2) MΘ§NΘ§P »ΐΒψΙ≤œΏΘ§ΟφΜΐΈΣ![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
1Θ©“‘OΈΣΉχ±ξ‘≠ΒψΘ§ABΥυ‘Ύ÷±œΏΈΣx÷αΘ§ΙΐO¥Ι÷±”ΎABΒΡ÷±œΏΈΣy÷αΘ§Ϋ®ΝΔ»γΆΦΥυ ΨΒΡΤΫΟφ÷±Ϋ«Ήχ±ξœΒΘ§OCΘΚyΘΫ1.5xΘΜODΘΚyΘΫ©¹0.5xΘ§…ηPΘ®aΘ§bΘ©Θ§MΘ®©¹2mΘ§mΘ©Θ§NΘ®nΘ§1.5nΘ©Θ§Θ®mΘΨ0Θ§nΘΨ0Θ©Θ§«σΫβΦ¥Ω…
Θ®2Θ©Ά®Ιΐ![]() ΆΤ≥ω
ΆΤ≥ω![]() Θ§άϊ”ΟΜυ±Ψ≤ΜΒ» Ϋ“‘ΦΑ»ΐΫ«–ΈΟφΜΐΙΪ ΫΦ¥Ω…
Θ§άϊ”ΟΜυ±Ψ≤ΜΒ» Ϋ“‘ΦΑ»ΐΫ«–ΈΟφΜΐΙΪ ΫΦ¥Ω…
Θ®1Θ©“‘OΈΣΉχ±ξ‘≠ΒψΘ§ABΥυ‘Ύ÷±œΏΈΣx÷αΘ§ΙΐO¥Ι÷±”ΎABΒΡ÷±œΏΈΣy÷αΘ§Ϋ®ΝΔ»γΆΦΥυ ΨΒΡΤΫΟφ÷±Ϋ«Ήχ±ξœΒΘ°‘ρCΘ®10Θ§15Θ©Θ§BΘ®10Θ§0Θ©Θ§DΘ®©¹30Θ§15Θ©Θ§PΘ®©¹4Θ§4Θ©Θ°OCΘΚyΘΫ1.5xΘΜODΘΚyΘΫ©¹0.5xΘ§
…ηPΘ®aΘ§bΘ©Θ§MΘ®©¹2mΘ§mΘ©Θ§NΘ®nΘ§1.5nΘ©Θ§Θ®mΘΨ0Θ§nΘΨ0Θ©Θ§
PΒΫOCΓΔODΒΡΨύάκΖ÷±πΈΣ![]() ΓΔ
ΓΔ![]() Θ§ΝΣΝΔΫβΖΫ≥ΧΉι
Θ§ΝΣΝΔΫβΖΫ≥ΧΉι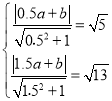 Θ§ΒΟ
Θ§ΒΟ![]() Θ§
Θ§
ΓΏPΈΣMNΒΡ÷–ΒψΘ§Υυ“‘![]() Θ§ΒΟm
Θ§ΒΟm![]() Θ§n
Θ§n![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Θ§
Θ§
ΓύdΘΫ|OM|![]() Θ°
Θ°
Θ®2Θ©”…MΘ§NΘ§P »ΐΒψΙ≤œΏΘ§ΒΟ![]() Θ§5m+6.5nΘΫ4mnΘ§Φ¥
Θ§5m+6.5nΘΫ4mnΘ§Φ¥![]() Θ§
Θ§
SΓςOMN![]() Θ§
Θ§
Θ®2m+nΘ©![]() Θ§Β±«“ΫωΒ±5n2ΘΫ13m2≥…ΝΔΘ§
Θ§Β±«“ΫωΒ±5n2ΘΫ13m2≥…ΝΔΘ§
Υυ“‘ΓςOMNΟφΜΐΉν–ΓΈΣ![]() Θ°
Θ°


 ΩΎΥψ–ΓΉ¥‘ΣΩΎΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗ
ΩΎΥψ–ΓΉ¥‘ΣΩΎΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“‘œ¬ΥΡΗωΟϋΧβΘΚ
ΔΌΓΑ»τ![]() Θ§‘ρ
Θ§‘ρ![]() Γ±ΒΡΡφΖώΟϋΧβΈΣ’φΟϋΧβ
Γ±ΒΡΡφΖώΟϋΧβΈΣ’φΟϋΧβ
ΔΎΓΑ![]() Γ± «ΓΑΚ· ΐ
Γ± «ΓΑΚ· ΐ![]() ‘Ύ«χΦδ
‘Ύ«χΦδ![]() …œΈΣ‘ωΚ· ΐΓ±ΒΡ≥δΖ÷≤Μ±Ί“ΣΧθΦΰ
…œΈΣ‘ωΚ· ΐΓ±ΒΡ≥δΖ÷≤Μ±Ί“ΣΧθΦΰ
Δέ»τ![]() ΈΣΦΌΟϋΧβΘ§‘ρ
ΈΣΦΌΟϋΧβΘ§‘ρ![]() Θ§
Θ§![]() ΨυΈΣΦΌΟϋΧβ
ΨυΈΣΦΌΟϋΧβ
ΔήΕ‘”ΎΟϋΧβ![]() ΘΚ
ΘΚ![]() Θ§
Θ§![]() Θ§‘ρ
Θ§‘ρ![]() ΈΣΘΚ
ΈΣΘΚ![]() Θ§
Θ§![]()
Τδ÷–’φΟϋΧβΒΡΗω ΐ «Θ® Θ©
A.1ΗωB.2ΗωC.3ΗωD.4Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΨΊ–Έ![]() Θ§
Θ§![]() ΤΫΟφ
ΤΫΟφ![]() Θ§
Θ§![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() Ζ÷±π «
Ζ÷±π «![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΒΡ÷–Βψ.
ΒΡ÷–Βψ.
Θ®1Θ©«σ÷ΛΘΚ÷±œΏ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©«σ÷ΛΘΚ÷±œΏ![]() ÷±œΏ
÷±œΏ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤![]() Θ§Ε®“εΆ÷‘≤
Θ§Ε®“εΆ÷‘≤![]() …œΒΡΒψ
…œΒΡΒψ![]() ΒΡΓΑΑιΥφΒψΓ±ΈΣ
ΒΡΓΑΑιΥφΒψΓ±ΈΣ![]() .
.
Θ®1Θ©«σΆ÷‘≤![]() …œΒΡΒψ
…œΒΡΒψ![]() ΒΡΓΑΑιΥφΒψΓ±
ΒΡΓΑΑιΥφΒψΓ±![]() ΒΡΙλΦΘΖΫ≥ΧΘΜ
ΒΡΙλΦΘΖΫ≥ΧΘΜ
Θ®2Θ©»γΙϊΆ÷‘≤![]() …œΒΡΒψ
…œΒΡΒψ![]() ΒΡΓΑΑιΥφΒψΓ±ΈΣ
ΒΡΓΑΑιΥφΒψΓ±ΈΣ![]() Θ§Ε‘”ΎΆ÷‘≤
Θ§Ε‘”ΎΆ÷‘≤![]() …œΒΡ»Έ“βΒψ
…œΒΡ»Έ“βΒψ![]() ΦΑΥϋΒΡΓΑΑιΥφΒψΓ±
ΦΑΥϋΒΡΓΑΑιΥφΒψΓ±![]() Θ§«σ
Θ§«σ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©Β±![]() Θ§
Θ§ ![]() ±Θ§÷±œΏ
±Θ§÷±œΏ![]() ΫΜΆ÷‘≤
ΫΜΆ÷‘≤![]() ”Ύ
”Ύ![]() Θ§
Θ§ ![]() ΝΫΒψΘ§»τΒψ
ΝΫΒψΘ§»τΒψ![]() Θ§
Θ§ ![]() ΒΡΓΑΑιΥφΒψΓ±Ζ÷±π «
ΒΡΓΑΑιΥφΒψΓ±Ζ÷±π «![]() Θ§
Θ§ ![]() Θ§«““‘
Θ§«““‘![]() ΈΣ÷±ΨΕΒΡ‘≤Ψ≠ΙΐΉχ±ξ‘≠Βψ
ΈΣ÷±ΨΕΒΡ‘≤Ψ≠ΙΐΉχ±ξ‘≠Βψ![]() Θ§«σ
Θ§«σ![]() ΒΡΟφΜΐΘ°
ΒΡΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
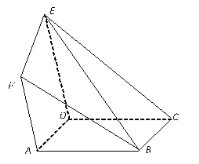
ΓΨΧβΡΩΓΩΈΣ≈ύ―χ―ß…ζΒΡ‘ΡΕΝœΑΙΏΘ§Ρ≥–ΘΩΣ’ΙΝΥΈΣΤΎ“ΜΡξΒΡΓΑΚκ―ο¥ΪΆ≥ΈΡΜ·Θ§‘ΡΕΝΨ≠ΒδΟϊ÷χΓ±ΜνΕ·. ΜνΕ·ΚσΘ§ΈΣΝΥΫβ‘ΡΕΝ«ιΩωΘ§―ß–ΘΆ≥ΦΤΝΥΦΉΓΔ““ΝΫΉιΗς10Οϊ―ß…ζΒΡ‘ΡΕΝΝΩΘ®ΒΞΈΜΘΚ±ΨΘ©Θ§Ά≥ΦΤΫαΙϊ”ΟΨΞ“ΕΆΦΦ«¬Φ»γœ¬Θ§““ΉιΦ«¬Φ÷–”–“ΜΗω ΐΨίΡΘΚΐΘ§ΈόΖ®»Ζ»œΘ§‘ΎΆΦ÷–“‘a±μ Ψ.
Θ®ΔώΘ©»τΦΉΉι‘ΡΕΝΝΩΒΡΤΫΨυ÷Β¥σ”Ύ““Ήι‘ΡΕΝΝΩΒΡΤΫΨυ÷ΒΘ§ «σΆΦ÷–aΒΡΥυ”–Ω…Ρή»Γ÷ΒΘΜ
Θ®ΔρΘ©ΫΪΦΉΓΔ““ΝΫΉι÷–‘ΡΕΝΝΩ≥§Ιΐ15±ΨΒΡ―ß…ζ≥ΤΈΣΓΑ‘ΡΕΝ¥ο»ΥΓ±. …η![]() Θ§œ÷¥”Υυ”–ΓΑ‘ΡΕΝ¥ο»ΥΓ±άο»Έ»Γ3»ΥΘ§«σΤδ÷–““ΉιΒΡ»Υ ΐXΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊ.
Θ§œ÷¥”Υυ”–ΓΑ‘ΡΕΝ¥ο»ΥΓ±άο»Έ»Γ3»ΥΘ§«σΤδ÷–““ΉιΒΡ»Υ ΐXΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊ.
Θ®ΔσΘ©Φ«ΦΉΉι‘ΡΕΝΝΩΒΡΖΫ≤νΈΣ![]() . ‘ΎΦΉΉι÷–‘ωΦ”“ΜΟϊ―ß…ζAΒΟΒΫ–¬ΒΡΦΉΉιΘ§»τAΒΡ‘ΡΕΝΝΩΈΣ10Θ§‘ρΦ«–¬ΦΉΉι‘ΡΕΝΝΩΒΡΖΫ≤νΈΣ
. ‘ΎΦΉΉι÷–‘ωΦ”“ΜΟϊ―ß…ζAΒΟΒΫ–¬ΒΡΦΉΉιΘ§»τAΒΡ‘ΡΕΝΝΩΈΣ10Θ§‘ρΦ«–¬ΦΉΉι‘ΡΕΝΝΩΒΡΖΫ≤νΈΣ![]() ΘΜ»τAΒΡ‘ΡΕΝΝΩΈΣ20Θ§‘ρΦ«–¬ΦΉΉι‘ΡΕΝΝΩΒΡΖΫ≤νΈΣ
ΘΜ»τAΒΡ‘ΡΕΝΝΩΈΣ20Θ§‘ρΦ«–¬ΦΉΉι‘ΡΕΝΝΩΒΡΖΫ≤νΈΣ![]() Θ§ ‘±»Ϋœ
Θ§ ‘±»Ϋœ![]() Θ§
Θ§![]() Θ§
Θ§![]() ΒΡ¥σ–Γ.Θ®Ϋα¬έ≤Μ“Σ«σ÷ΛΟςΘ©
ΒΡ¥σ–Γ.Θ®Ϋα¬έ≤Μ“Σ«σ÷ΛΟςΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΆ≈ΧεΙΚ¬ρΙΪ‘ΑΟ≈Τ±Θ§Τ±Φέ»γœ¬±μΘΚ
ΙΚΤ±»Υ ΐ | 1~50 | 51~100 | 100“‘…œ |
Ο≈Τ±ΦέΗώ | 13‘Σ/»Υ | 11‘Σ/»Υ | 9‘Σ/»Υ |
œ÷Ρ≥ΒΞΈΜ“ΣΉι÷·Τδ –≥Γ≤ΩΚΆ…ζ≤ζ≤ΩΒΡ‘±ΙΛ”ΈάάΗΟΙΪ‘ΑΘ§’βΝΫΗω≤ΩΟ≈»Υ ΐΖ÷±πΈΣaΚΆb![]() Θ§»τΑ¥≤ΩΟ≈ΉςΈΣΆ≈ΧεΘ§―Γ‘ώΝΫΗω≤ΜΆ§ΒΡ ±ΦδΖ÷±πΙΚΤ±”ΈάάΙΪ‘ΑΘ§‘ρΙ≤–η÷ßΗΕΟ≈Τ±Ζ―ΈΣ1290‘ΣΘΜ»τΝΫΗω≤ΩΟ≈Κœ‘Ύ“ΜΤπΉςΈΣ“ΜΗωΆ≈ΧεΘ§Ά§“Μ ±ΦδΙΚΤ±”ΈάάΙΪ‘ΑΘ§‘ρ–η÷ßΗΕΟ≈Τ±Ζ―ΈΣ990‘ΣΘ§Ρ«Ο¥’βΝΫΗω≤ΩΟ≈ΒΡ»Υ ΐ
Θ§»τΑ¥≤ΩΟ≈ΉςΈΣΆ≈ΧεΘ§―Γ‘ώΝΫΗω≤ΜΆ§ΒΡ ±ΦδΖ÷±πΙΚΤ±”ΈάάΙΪ‘ΑΘ§‘ρΙ≤–η÷ßΗΕΟ≈Τ±Ζ―ΈΣ1290‘ΣΘΜ»τΝΫΗω≤ΩΟ≈Κœ‘Ύ“ΜΤπΉςΈΣ“ΜΗωΆ≈ΧεΘ§Ά§“Μ ±ΦδΙΚΤ±”ΈάάΙΪ‘ΑΘ§‘ρ–η÷ßΗΕΟ≈Τ±Ζ―ΈΣ990‘ΣΘ§Ρ«Ο¥’βΝΫΗω≤ΩΟ≈ΒΡ»Υ ΐ![]() ____ΘΜ
____ΘΜ![]() ____.
____.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΕύΟφΧε![]() ÷–Θ§ΒΉΟφ
÷–Θ§ΒΉΟφ![]() ΈΣΨΊ–ΈΘ§≤ύΟφ
ΈΣΨΊ–ΈΘ§≤ύΟφ![]() ΈΣΧί–ΈΘ§
ΈΣΧί–ΈΘ§![]() Θ§
Θ§![]() Θ§
Θ§![]() .
.
Θ®ΔώΘ©«σ÷ΛΘΚ![]() ΘΜ
ΘΜ
Θ®ΔρΘ©«σ÷ΛΘΚ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®ΔσΘ©≈–ΕœœΏΕΈ![]() …œ «Ζώ¥φ‘ΎΒψ
…œ «Ζώ¥φ‘ΎΒψ![]() Θ§ ΙΒΟΤΫΟφ
Θ§ ΙΒΟΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΩ≤ΔΥΒΟςάμ”…Θ°
ΘΩ≤ΔΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥÷–―ßΈΣΝΥΉιΫ®“Μ÷ß“Β”ύΉψ«ρΕ”Θ§‘ΎΗΏ“ΜΡξΦΕΥφΜζ―Γ»Γ50ΟϊΡ–…ζ≤βΝΩ…μΗΏΘ§ΖΔœ÷±Μ≤βΡ–…ζΒΡ…μΗΏ»Ϊ≤Ω‘Ύ![]() ΒΫ
ΒΫ![]() ÷°ΦδΘ§ΫΪ≤βΝΩΫαΙϊΑ¥»γœ¬ΖΫ ΫΖ÷≥…ΝυΉιΘΚΒΎ1Ήι
÷°ΦδΘ§ΫΪ≤βΝΩΫαΙϊΑ¥»γœ¬ΖΫ ΫΖ÷≥…ΝυΉιΘΚΒΎ1Ήι![]() Θ§ΒΎ2Ήι
Θ§ΒΎ2Ήι![]() Θ§Γ≠Θ§ΒΎ6Ήι
Θ§Γ≠Θ§ΒΎ6Ήι![]() Θ§»γΆΦ «Α¥…œ ωΖ÷ΉιΒΟΒΫΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§“‘ΤΒ¬ ΫϋΥΤΗ≈¬ .
Θ§»γΆΦ «Α¥…œ ωΖ÷ΉιΒΟΒΫΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§“‘ΤΒ¬ ΫϋΥΤΗ≈¬ .
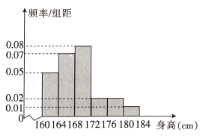
Θ®1Θ©»τ―ß–Θ“Σ¥”÷–―Γ1ΟϊΡ–…ζΒΘ»ΈΉψ«ρΕ”≥ΛΘ§«σ±Μ―Γ»ΓΒΡΡ–…ζ«ΓΚΟ‘ΎΒΎ5ΉιΜρΒΎ6ΉιΒΡΗ≈¬ ΘΜ
Θ®2Θ© ‘ΙάΦΤΗΟ–ΘΗΏ“ΜΡξΦΕ»ΪΧεΡ–…ζ…μΗΏΒΡΤΫΨυ ΐΘ®Ά§“ΜΉι÷–ΒΡ ΐΨί”ΟΗΟΉι«χΦδΒΡ÷–Βψ÷Β¥ζ±μΘ©”κ÷–ΈΜ ΐΘΜ
Θ®3Θ©œ÷‘Ύ¥”ΒΎ5”κΒΎ6ΉιΡ–…ζ÷–―Γ»ΓΝΫΟϊΆ§―ßΒΘ»Έ ΊΟ≈‘±Θ§«σ―Γ»ΓΒΡΝΫ»Υ÷–ΉνΕύ”–1ΟϊΡ–…ζά¥Ή‘ΒΎ5ΉιΒΡΗ≈¬ .
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ![]() «Ή‘»ΜΕ‘ ΐΒΡΒΉ ΐΘ§Κ· ΐ
«Ή‘»ΜΕ‘ ΐΒΡΒΉ ΐΘ§Κ· ΐ![]() ”κ
”κ![]() ΒΡΕ®“ε”ρΕΦ «
ΒΡΕ®“ε”ρΕΦ «![]() .
.
Θ®1Θ©«σΚ· ΐ![]() ‘ΎΒψ
‘ΎΒψ![]() ¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
Θ®2Θ©«σ÷ΛΘΚΚ· ΐ![]() ÷Μ”–“ΜΗωΝψΒψ
÷Μ”–“ΜΗωΝψΒψ![]() Θ§«“
Θ§«“![]() ΘΜ
ΘΜ
Θ®3Θ©”Ο![]() ±μ Ψ
±μ Ψ![]() Θ§
Θ§![]() ΒΡΉν–Γ÷ΒΘ§…η
ΒΡΉν–Γ÷ΒΘ§…η![]() Θ§
Θ§![]() Θ§»τΚ· ΐ
Θ§»τΚ· ΐ![]() ‘Ύ
‘Ύ![]() …œΈΣ‘ωΚ· ΐΘ§«σ Β ΐ
…œΈΣ‘ωΚ· ΐΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com