
【题目】设函数![]() (
(![]() 且
且![]() ),当点
),当点![]() 是函数
是函数![]() 图象上的点时,点
图象上的点时,点![]() 是函数
是函数![]() 图象上的点.
图象上的点.
(1)写出函数![]() 的解析式;
的解析式;
(2)把![]() 的图象向左平移
的图象向左平移![]() 个单位得到
个单位得到![]() 的图象,函数
的图象,函数![]() ,是否存在实数
,是否存在实数![]() ,使函数
,使函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() .如果存在,求出
.如果存在,求出![]() 的值;如果不存在,说明理由;
的值;如果不存在,说明理由;
(3)若当![]() 时,恒有
时,恒有![]() ,试确定
,试确定![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】试题分析:(1)设点Q的坐标为![]() ,利用
,利用![]() =x-2a,
=x-2a, ![]() =-y,转化x=
=-y,转化x=![]() +2a,y=-
+2a,y=-![]() .通过点P(x,y)在函数y=loga(x-3a)图象上,代入即可得到函数y=g(x)的解析式;
.通过点P(x,y)在函数y=loga(x-3a)图象上,代入即可得到函数y=g(x)的解析式;
(2) ![]() ,因为
,因为![]() ,故
,故![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增, 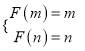 ,即
,即![]() 为
为![]() 的两相异的非负的实数,解方程即得
的两相异的非负的实数,解方程即得![]() 的值;
的值;
(3) 通过![]() ,求出
,求出![]() 的最大值,利用最大值≤1,即可确定
的最大值,利用最大值≤1,即可确定![]() 的取值范围;
的取值范围;
试题解析:
(1)解:设点![]() 的坐标为
的坐标为![]() ,
,
则![]() ,即
,即![]() .
.
![]() 点
点![]() 在函数
在函数![]() 图象上,
图象上,
![]() ,即
,即![]() ,
,
![]() .
.
(2)![]() ,
,
![]() ,故
,故![]()
![]() 在
在![]() 上单调递增,
上单调递增, 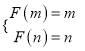 ,即
,即![]() 为
为![]() 的两相异的非负的实数
的两相异的非负的实数
即![]() ,解得
,解得![]() .
.
(3)函数![]() ,
,
由题意![]() ,则
,则![]() ,
,
又![]() ,且
,且![]()
![]() ,
,
![]() ,
,
又![]() 对称轴为
对称轴为![]() ,
,
![]() ,则
,则![]() 在
在![]() 上为增函数,
上为增函数,
![]() 函数
函数![]() 在
在![]() 上为减函数,
上为减函数,
从而![]() ,
,
又![]() ,则
,则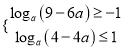 ,
,
![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,且
,且![]() ).
).
(1)当![]() 时,设集合
时,设集合![]() ,求集合
,求集合![]() ;
;
(2)在(1)的条件下,若![]() ,且满足
,且满足![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若对任意的![]() ,存在
,存在![]() ,使不等式
,使不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下判断: ①f(x)= ![]() 与g(x)=
与g(x)= ![]() 表示同一函数;
表示同一函数;
②函数y=f(x)的图象与直线x=1的交点最多有1个;
③f(x)=x2﹣2x+1与g(t)=t2﹣2t+1是同一函数;
④若f(x)=|x﹣1|﹣|x|,则f(f( ![]() ))=0.
))=0.
其中正确判断的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题。
(1)已知f( ![]() +1)=x+2
+1)=x+2 ![]() ,求f(x)的解析式;
,求f(x)的解析式;
(2)已知f(x)是一次函数,且满足3f(x+1)﹣2f(x﹣1)=2x+17,求f(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接党的“十九大”胜利召开与响应国家交给的“提速降费”任务,某市移动公司欲提供新的资费套餐(资费包含手机月租费、手机拨打电话费与家庭宽带上网费)。其中一组套餐变更如下:
原方案资费
手机月租费 | 手机拨打电话 | 家庭宽带上网费(50M) |
18元/月 | 0.2元/分钟 | 50元/月 |
新方案资费
手机月租费 | 手机拨打电话 | 家庭宽带上网费(50M) |
58元/月 | 前100分钟免费, 超过部分 | 免费 |
(1)客户甲(只有一个手机号和一个家庭宽带上网号)欲从原方案改成新方案,设其每月手机通话时间为![]() 分钟(
分钟(![]() ),费用
),费用![]() 原方案每月资费-新方案每月资费,写出
原方案每月资费-新方案每月资费,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)经过统计,移动公司发现,选这组套餐的客户平均月通话时间![]() 分钟,为能起到降费作用,求
分钟,为能起到降费作用,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com