Question

【题目】已知椭圆的长轴长为，离心率为.

(1)求椭圆的方程；

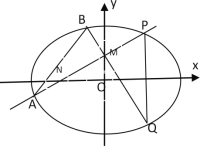
(2)过动点的直线交轴于点，交椭圆于点，(在第一象限)，且是线段的中点.过点作轴的垂线交椭圆于另一点，延长交椭圆于点.

①设直线、的斜率分别为，证明为定值;

②求直线斜率取最小值时，直线的方程.

Answer 1

【答案】（1）（2）①详见解析②

【解析】

(1) 利用长轴长为，离心率为分别求出的值，再求出的值，即可求出椭圆方程；(2) ① 设出的坐标，表示出直线的斜率，作比即可；②设出的坐标，分别求出的方程，联立方程组，求出直线的斜率的解析式，根据不等式的性质计算出的最小值，再求出的值即可.

（1）由题意得：，

所以，，

故椭圆方程为.

（2）①设，（，），由，可得，

所以直线的斜率，直线的斜率

此时，所以为定值.

②设，，直线的方程为，直线的方程为.

联立，整理得，

由，可得，

同理，.

所以，，

，

所以，

由，，可知，所以，当且仅当时取得等号.

由，，在椭圆：上得，

此时，即，

由得，，所以时，符合题意.

所以直线的斜率最小时，直线的方程为.