
【题目】抚州市某中学利用周末组织教职员工进行了一次秋季登军峰山健身的活动,有![]() 人参加,现将所有参加人员按年龄情况分为
人参加,现将所有参加人员按年龄情况分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 等七组,其频率分布直方图如下图所示.已知
等七组,其频率分布直方图如下图所示.已知![]() 之间的参加者有4人.
之间的参加者有4人.
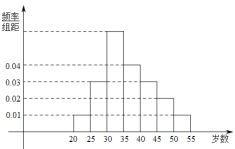
(1)求![]() 和
和![]() 之间的参加者人数
之间的参加者人数![]() ;
;
(2)组织者从![]() 之间的参加者(其中共有
之间的参加者(其中共有![]() 名女教师包括甲女,其余全为男教师)中随机选取
名女教师包括甲女,其余全为男教师)中随机选取![]() 名担任后勤保障工作,求在甲女必须入选的条件下,选出的女教师的人数为2人的概率.
名担任后勤保障工作,求在甲女必须入选的条件下,选出的女教师的人数为2人的概率.
(3)已知![]() 和
和![]() 之间各有
之间各有![]() 名数学教师,现从这两个组中各选取
名数学教师,现从这两个组中各选取![]() 人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有
人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有![]() 名数学教师的概率?
名数学教师的概率?
【答案】(1)![]() ,
,![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)先根据频率分布直方图求出年龄在![]() 和
和![]() 内的频率,再根据样本总数=频数/频率,即可求出
内的频率,再根据样本总数=频数/频率,即可求出![]() 和
和![]() ;(2)根据古典概型的概率计算公式,通过列举,分别求出“在甲女必须入选的条件下”的基本事件总数,“在甲女必须入选的条件下,选出的女教师的人数为2人”的事件数,即可算出概率;(3)根据相互独立事件同时发生的概率公式,只需分别求出两组各自选取两人中至少有一名数学老师的概率,相乘即可求出。
;(2)根据古典概型的概率计算公式,通过列举,分别求出“在甲女必须入选的条件下”的基本事件总数,“在甲女必须入选的条件下,选出的女教师的人数为2人”的事件数,即可算出概率;(3)根据相互独立事件同时发生的概率公式,只需分别求出两组各自选取两人中至少有一名数学老师的概率,相乘即可求出。
(1)由题可知,![]() ,故
,故![]() ,
,
而![]() ,则
,则![]()
(2)由题可知![]() ,则有4名女教师和2名男教师,设女教师为甲,乙,丙,丁,男教师为A,B,从中随机选取3名担任后勤保障工作,由于甲女一定入选,所以只需从剩下的5名老师中选取2名,基本事件有如下10种情况,(乙丙)(乙丁)(乙A)(乙B)(丙丁)(丙A)(丙B)(丁A)(丁B)(AB),其中恰有2女教师的有(乙A)(乙B)(丙A)(丙B)(丁A)(丁B)共6种情况,故
,则有4名女教师和2名男教师,设女教师为甲,乙,丙,丁,男教师为A,B,从中随机选取3名担任后勤保障工作,由于甲女一定入选,所以只需从剩下的5名老师中选取2名,基本事件有如下10种情况,(乙丙)(乙丁)(乙A)(乙B)(丙丁)(丙A)(丙B)(丁A)(丁B)(AB),其中恰有2女教师的有(乙A)(乙B)(丙A)(丙B)(丁A)(丁B)共6种情况,故![]()
(3)由题可知,![]() ,
,![]() ,所以
,所以![]()
![]() ,而两组的选择互不影响,所以互为独立事件,故
,而两组的选择互不影响,所以互为独立事件,故![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠DAB=60°.
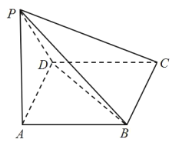
(1)证明:AD⊥PB.
(2)若PB=![]() ,AB=PA=2,求三棱锥P-BCD的体积。
,AB=PA=2,求三棱锥P-BCD的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,己知圆
中,己知圆![]() ,且圆
,且圆![]() 被直线
被直线![]() 截得的弦长为2.
截得的弦长为2.
(1)求圆![]() 的标准方程;
的标准方程;
(2)若圆![]() 的切线
的切线![]() 在
在![]() 轴和
轴和![]() 轴上的截距相等,求切线
轴上的截距相等,求切线![]() 的方程;
的方程;
(3)若圆![]() 上存在点
上存在点![]() ,由点
,由点![]() 向圆
向圆![]() 引一条切线,切点为
引一条切线,切点为![]() ,且满足
,且满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为
的长轴长为![]() ,焦距为2,抛物线
,焦距为2,抛物线![]() 的准线经过
的准线经过![]() 的左焦点
的左焦点![]() .
.
(1)求![]() 与
与![]() 的方程;
的方程;
(2)直线![]() 经过
经过![]() 的上顶点且
的上顶点且![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 与
与![]() 分别交于点
分别交于点![]() (异于点
(异于点![]() ),
),![]() (异于点
(异于点![]() ),证明:直线
),证明:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调研机构,对本地![]() 岁的人群随机抽取
岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,结果显示,有
人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,结果显示,有![]() 人为“低碳族”,该
人为“低碳族”,该![]() 人的年龄情况对应的频率分布直方图如图.
人的年龄情况对应的频率分布直方图如图.
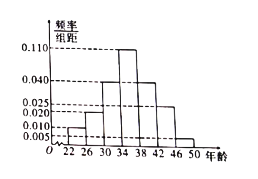
(1)根据频率分布直方图,估计这![]() 名“低碳族”年龄的平均值,中位数;
名“低碳族”年龄的平均值,中位数;
(2)若在“低碳族”且年龄在![]() 、
、![]() 的两组人群中,用分层抽样的方法抽取
的两组人群中,用分层抽样的方法抽取![]() 人,试估算每个年龄段应各抽取多少人?
人,试估算每个年龄段应各抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数)曲线
为参数)曲线![]() 的普通方程为
的普通方程为![]() ,以坐标原点为极点,以
,以坐标原点为极点,以![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 和曲线
和曲线![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() :
:![]() 依次与曲线
依次与曲线![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点,射线
两点,射线![]() :
:![]() 依次与曲线
依次与曲线![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com