
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,画出函数
时,画出函数![]() 的大致图像;
的大致图像;
(2)当![]() 时,根据图像写出函数
时,根据图像写出函数![]() 的单调减区间,并用定义证明你的结论;
的单调减区间,并用定义证明你的结论;
(3)试讨论关于x的方程![]() 解的个数.
解的个数.

【答案】详见解析
【解析】
(1)当![]() 时,将函数化为
时,将函数化为![]() ,由此画出函数的图像.(2)根据(1)的图像写出函数的单调减区间,利用单调性的定义,通过计算
,由此画出函数的图像.(2)根据(1)的图像写出函数的单调减区间,利用单调性的定义,通过计算![]() ,证得函数单调性.(3)
,证得函数单调性.(3)![]() ,由于
,由于![]() ,故函数
,故函数![]() 图像与(1)中的图像类似.将方程
图像与(1)中的图像类似.将方程![]() 解的个数问题转化为
解的个数问题转化为![]() 与
与![]() 图像的交点个数来解.将
图像的交点个数来解.将![]() 分成
分成![]() 五种情况,讨论两个函数交点的个数.
五种情况,讨论两个函数交点的个数.
(1)如图所示
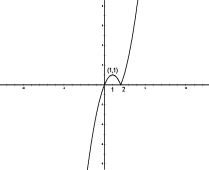
(2)![]() 单调递减区间:
单调递减区间:![]()
证明:设任意的![]()
![]()
![]()
![]()
因为![]() ,所以
,所以![]()
于是![]() ,即
,即![]()
所以函数![]() 在
在![]() 上是单调递减函数
上是单调递减函数
(3) 由题意知方程![]() 的解得个数等价于函数
的解得个数等价于函数![]() 的图像与直线
的图像与直线![]() 的交点个数.即函数
的交点个数.即函数![]() 的图象与直线
的图象与直线![]() 的交点个数
的交点个数
又![]() ,注意到
,注意到![]() ,
,
当且仅当![]() 时,上式等号成立,借助图像知
时,上式等号成立,借助图像知
所以,当![]() 时,函数
时,函数![]() 的图像与直线
的图像与直线![]() 有1个交点;
有1个交点;
当![]() ,
,![]() 时,函数
时,函数![]() 的图像与直线
的图像与直线![]() 有2个交点;
有2个交点;
当![]() ,
,![]() 时,函数
时,函数![]() 的图像与直线
的图像与直线![]() 有3个交点;
有3个交点;


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c.若sin(A﹣B)+sinC= ![]() sinA.
sinA.
(1)求角B的值;
(2)若b=2,求a2+c2的最大值,并求取得最大值时角A,C的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知y=f′(x)的图象如图所示,若两个正数a,b满足f(2a+b)<1,则![]() 的取值范围是____.
的取值范围是____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,满足c=1,且cosBsinC+(a﹣sinB)cos(A+B)=0
(1)求C的大小;
(2)求a2+b2的最大值,并求取得最大值时角A,B的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某重点中学100位学生在市统考中的理科综合分数,以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求理科综合分数的众数和中位数;
(3)在理科综合分数为![]() ,
, ![]() ,
, ![]() ,
, ![]() 的四组学生中,用分层抽样的方法抽取11名学生,则理科综合分数在
的四组学生中,用分层抽样的方法抽取11名学生,则理科综合分数在![]() 的学生中应抽取多少人?
的学生中应抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为 ![]() (t为参数),在以直角坐标系的原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ=
(t为参数),在以直角坐标系的原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ= ![]()
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)若直线l与曲线C相交于A,B两点,求△AOB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣e﹣x﹣2x.
(1)讨论f(x)的单调性;
(2)设g(x)=f(2x)﹣4bf(x),当x>0时,g(x)>0,求b的最大值;
(3)已知1.4142< ![]() <1.4143,估计ln2的近似值(精确到0.001).
<1.4143,估计ln2的近似值(精确到0.001).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com