
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() ,
,![]() ,且存在不相等的实数
,且存在不相等的实数![]() ,使得
,使得![]() ,求证
,求证![]() 且
且![]() .
.
【答案】(1)函数单调性见解析;(2)证明见解析.
【解析】
(1)分别在![]() 和
和![]() 两种情况下讨论导函数的正负,进而得到函数的单调性;
两种情况下讨论导函数的正负,进而得到函数的单调性;
(2)当![]() 时,可通过放缩知
时,可通过放缩知![]() ,知其不符合题意,得到
,知其不符合题意,得到![]() ;由
;由![]() 和
和![]() 时,
时,![]() 可得到
可得到![]() ,将所证不等式化为
,将所证不等式化为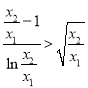 ,令
,令![]() ,利用导数可求得
,利用导数可求得![]() ,进而证得结论.
,进而证得结论.
(1)由题意得:![]() 定义域为
定义域为![]() ,
,![]() ,
,
令![]() ,则
,则![]() ,
,
①当![]() ,即
,即![]() 时,
时,![]() ,
,![]() ,
,
![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() ,即
,即![]() 时,
时,
令![]() ,解得:
,解得:![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 当
当![]() 和
和![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上恒成立,
上恒成立,
![]() 在
在![]() 上单调递增;
上单调递增;
综上所述:当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在 ,
,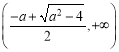 上单调递增,在
上单调递增,在 上单调递减.
上单调递减.
(2)由题意得:![]() ,则
,则![]() ;
;
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递增,与存在不相等的实数
上单调递增,与存在不相等的实数![]() 使得
使得![]() 相矛盾,
相矛盾,
![]() .
.
由![]() 得:
得:![]() ,
,
![]() ,
,
不妨设![]() ,
,
令![]() ,则
,则![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增,![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
欲证![]() ,只需证
,只需证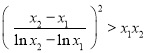 ,只需证
,只需证![]() ,
,
即证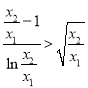 ,
,
令![]() ,则只需证
,则只需证![]() ,即证
,即证![]() ,
,
令![]() ,
,
则 ,
,
![]() 在
在![]() 上单调递减,
上单调递减,![]() ,从而
,从而![]() 得证,
得证,
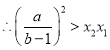 .
.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 的底面
的底面![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点,且
的中点,且![]()
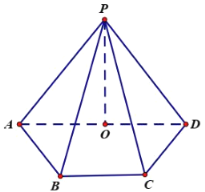
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在线段![]() 内是否存在点
内是否存在点![]() ,使得
,使得![]() ?若存在指出点
?若存在指出点![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,
,![]() 为椭圆上一动点(异于左右顶点),
为椭圆上一动点(异于左右顶点),![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 相交于点
相交于点![]() 两点,问
两点,问![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形?若存在,求点
为直角顶点的等腰直角三角形?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司订购了一批树苗,为了检测这批树苗是否合格,从中随机抽测![]() 株树苗的高度,经数据处理得到如图1所示的频率分布直方图,其中最高的
株树苗的高度,经数据处理得到如图1所示的频率分布直方图,其中最高的![]() 株树苗的高度的茎叶图如图2所示,以这
株树苗的高度的茎叶图如图2所示,以这![]() 株树苗的高度的频率估计整批树苗高度的概率.
株树苗的高度的频率估计整批树苗高度的概率.
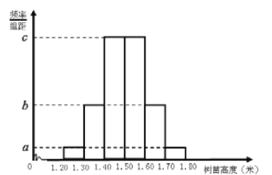

(1)求这批树苗的高度于![]() 米的概率,并求图
米的概率,并求图![]() 中
中![]() 的值;
的值;
(2)若从这批树苗中随机选取![]() 株,记
株,记![]() 为高度在
为高度在![]() 的树苗数量,求
的树苗数量,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若变量![]() 满足
满足![]() 且
且![]() ,则称变量
,则称变量![]() 满足近似于正态分布
满足近似于正态分布![]() 的概率分布,如果这批树苗的高度近似于正态分布
的概率分布,如果这批树苗的高度近似于正态分布![]() 的概率分布,则认为这批树苗是合格的,将顺利被签收,否则,公司将拒绝签收.试问:该批树苗是否被签收?
的概率分布,则认为这批树苗是合格的,将顺利被签收,否则,公司将拒绝签收.试问:该批树苗是否被签收?
查看答案和解析>>
科目:高中数学 来源: 题型:
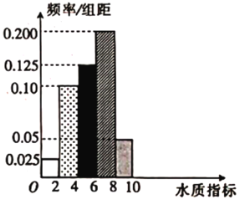
【题目】新《水污染防治法》已由中华人民共和国第十二届全国人民代表大会常务委员会第二十八次会议于2017年6月27日通过,自2018年1月1日起施行.2018年3月1日,某县某质检部门随机抽取了县域内100眼水井,检测其水质总体指标.
罗斯水质指数 | 02 | 24 | 46 | 68 | 810 |
水质状况 | 腐败污水 | 严重污染 | 污染 | 轻度污染 | 纯净 |
(1)求所抽取的100眼水井水质总体指标值的样本平均数![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).
(2)①由直方图可以认为,100眼水井水质总体指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在(5.21,5.99)内的概率;
落在(5.21,5.99)内的概率;
②将频率视为概率,若某乡镇抽查5眼水井的水质,记这5眼水井水质总体指标值位于(6,10)内的井数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100眼水井总体指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型公司为了切实保障员工的健康安全,贯彻好卫生防疫工作的相关要求,决定在全公司范围内举行一次乙肝普查.为此需要抽验669人的血样进行化验,由于人数较多,检疫部门制定了下列两种可供选择的方案.
方案一:将每个人的血分别化验,这时需要验669次.
方案二:按![]() 个人一组进行随机分组,把从每组
个人一组进行随机分组,把从每组![]() 个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这
个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这![]() 个人的血就只需检验一次(这时认为每个人的血化验
个人的血就只需检验一次(这时认为每个人的血化验![]() 次);否则,若呈阳性,则需对这
次);否则,若呈阳性,则需对这![]() 个人的血样再分别进行一次化验,这时该组
个人的血样再分别进行一次化验,这时该组![]() 个人的血总共需要化验
个人的血总共需要化验![]() 次.
次.
假设此次普查中每个人的血样化验呈阳性的概率为![]() ,且这些人之间的试验反应相互独立.
,且这些人之间的试验反应相互独立.
(1)设方案二中,某组![]() 个人中每个人的血化验次数为
个人中每个人的血化验次数为![]() ,求
,求![]() 的分布列.
的分布列.
(2)设![]() ,试比较方案二中,
,试比较方案二中,![]() 分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案一,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案一,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com