
【题目】在四棱锥![]() 的底面
的底面![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点,且
的中点,且![]()
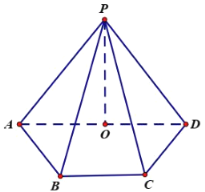
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在线段![]() 内是否存在点
内是否存在点![]() ,使得
,使得![]() ?若存在指出点
?若存在指出点![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
【答案】(1)证明见解析; (2)![]() ; (3)线段
; (3)线段![]() 上存在中点
上存在中点![]() ,使得
,使得![]() .
.
【解析】
(1)连接![]() ,证得四边形
,证得四边形![]() 为平行四边形,得到
为平行四边形,得到![]() ,利用线面平行的判定定理,即可证得
,利用线面平行的判定定理,即可证得![]() ∥平面
∥平面![]() ;
;
(2)建立空间直角坐标系,求得平面![]() 和平面
和平面![]() 的法向量,利用向量的夹角公式,即可求解;
的法向量,利用向量的夹角公式,即可求解;
(3)假设存在,设出点E的坐标,通过![]() 时,向量的数量积为0,建立方程,即可求解.
时,向量的数量积为0,建立方程,即可求解.
(1)连接![]() ,因为
,因为![]() 是
是![]() 的中点,
的中点,![]() ,
,
所以![]() ,且
,且![]() ,
,
所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ∥平面
∥平面![]() ;
;
(2)由(1)可知,四边形![]() 也是平行四边形,
也是平行四边形,
又由![]() ,所以四边形
,所以四边形![]() 是正方形,所以
是正方形,所以![]() ,
,
又由![]() 平面
平面![]() ,所以以O为原点,
,所以以O为原点,![]() 所在的直线分别为
所在的直线分别为![]() 轴,建立如图所示的空间直角坐标系,则
轴,建立如图所示的空间直角坐标系,则![]() ,
,
可得![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则 ,可取
,可取![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则 ,可取
,可取![]() ,
,
设二面角![]() 的平面角为
的平面角为 ,
,
即二面角![]() 的余弦值为
的余弦值为![]() .
.
(3)假设线段![]() 上存在点E,且满足
上存在点E,且满足![]() ,
,
设![]() ,则
,则![]() ,所以
,所以 ,即
,即![]() ,
,
所以![]() ,
,
又由![]() ,可得
,可得![]() ,
,
所以![]() ,解得
,解得![]() ,
,
即线段![]() 上存在中点
上存在中点![]() ,使得
,使得![]() .
.



 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() :
:![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,
,![]() ,
,![]() 是曲线
是曲线![]() 上的动点,求
上的动点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a=2![]() ,_______,求△ABC的周长l的范围.
,_______,求△ABC的周长l的范围.
在①![]() (﹣cos
(﹣cos![]() ,sin
,sin![]() ),
),![]() (cos
(cos![]() ,sin
,sin![]() ),且
),且![]()
![]() ,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x
,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x![]() )
)![]() ,f(A)
,f(A)![]()
注:这三个条件中任选一个,补充在上面问题中并对其进行求解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知自变量为![]() 的函数
的函数![]() .其中
.其中![]() ,
,![]() 为自然对数的底,
为自然对数的底,![]() .
.
(Ⅰ)求函数![]() 与
与![]() 的单调区间,并且讨论函数
的单调区间,并且讨论函数![]() 的单调性;
的单调性;
(Ⅱ)已知![]() ,求证:
,求证:
(ⅰ)方程![]() 有两个根
有两个根![]() ,
,![]() ;
;
(ⅱ)若(ⅰ)中的两个根满足![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
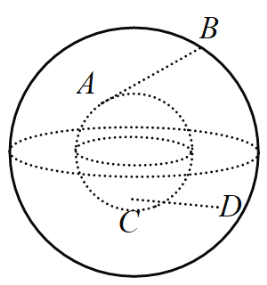
【题目】如图两个同心球,球心均为点![]() ,其中大球与小球的表面积之比为3:1,线段
,其中大球与小球的表面积之比为3:1,线段![]() 与
与![]() 是夹在两个球体之间的内弦,其中
是夹在两个球体之间的内弦,其中![]() 两点在小球上,
两点在小球上,![]() 两点在大球上,两内弦均不穿过小球内部.当四面体
两点在大球上,两内弦均不穿过小球内部.当四面体![]() 的体积达到最大值时,此时异面直线
的体积达到最大值时,此时异面直线![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图(甲)所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图(乙)所示.
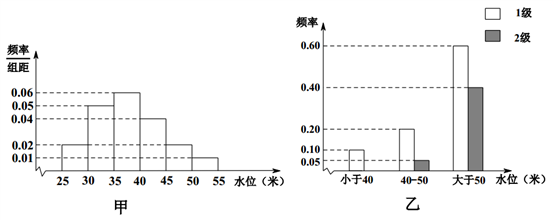
试估计该河流在8月份水位的中位数;
(1)以此频率作为概率,试估计该河流在8月份发生1级灾害的概率;
(2)该河流域某企业,在8月份,若没受1、2级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.
现此企业有如下三种应对方案:
方案 | 防控等级 | 费用(单位:万元) |
方案一 | 无措施 | 0 |
方案二 | 防控1级灾害 | 40 |
方案三 | 防控2级灾害 | 100 |
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com