
【题目】已知函数![]() .
.
(1)当![]() 时,判断
时,判断![]() 在
在![]() 上的单调性并加以证明;
上的单调性并加以证明;
(2)若![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 在
在![]() 为增函数;证明见解析(2)
为增函数;证明见解析(2)![]()
【解析】
(1)令![]() ,求出
,求出![]() ,可推得
,可推得![]() ,故
,故![]() 在
在![]() 为增函数;
为增函数;
(2)令![]() ,则
,则![]() ,由此利用分类讨论思想和导数性质求出实数
,由此利用分类讨论思想和导数性质求出实数![]() 的取值范围.
的取值范围.
(1)当![]() 时,
时,![]() .
.
记![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() .
.
所以![]() ,所以
,所以![]() 在
在![]() 单调递增,所以
单调递增,所以![]() .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 为增函数.
为增函数.
(2)由题意,得![]() ,记
,记![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 为增函数,即
为增函数,即![]() 在
在![]() 单调递增,
单调递增,
所以![]() .
.
①当![]() ,
,![]() ,
,![]() 恒成立,所以
恒成立,所以![]() 为增函数,即
为增函数,即![]() 在
在![]() 单调递增,
单调递增,
又![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 为增函数,所以
为增函数,所以![]()
所以![]() 满足题意.
满足题意.
②当![]() ,
,![]() ,令
,令![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,故
,故![]() 在
在![]() 单调递增,
单调递增,
故![]() ,即
,即![]() .
.
故![]() ,
,
又![]() 在
在![]() 单调递增,
单调递增,
由零点存在性定理知,存在唯一实数![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减,即
单调递减,即![]() 单调递减,
单调递减,
所以![]() ,此时
,此时![]() 在
在![]() 为减函数,
为减函数,
所以![]() ,不合题意,应舍去.
,不合题意,应舍去.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
【题目】按照下列要求,分别求有多少种不同的方法?
(1)5个不同的小球放入3个不同的盒子;
(2)5个不同的小球放入3个不同的盒子,每个盒子至少一个小球;
(3)5个相同的小球放入3个不同的盒子,每个盒子至少一个小球;
(4)5个不同的小球放入3个不同的盒子,恰有1个空盒.
查看答案和解析>>
科目:高中数学 来源: 题型:
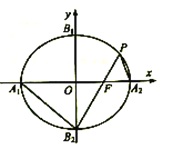
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的右焦点为
的右焦点为![]() ,左、右顶点分别为
,左、右顶点分别为![]() 、
、![]() ,上、下顶点分别为
,上、下顶点分别为![]() 、
、![]() ,连结
,连结![]() 并延长交椭圆于点
并延长交椭圆于点![]() ,连结
,连结![]() ,
,![]() ,记椭圆
,记椭圆![]() 的离心率为
的离心率为![]() .
.
(1)若![]() ,
,![]() .
.
①求椭圆![]() 的标准方程;
的标准方程;
②求![]() 和
和![]() 的面积之比.
的面积之比.
(2)若直线![]() 和直线
和直线![]() 的斜率之积为
的斜率之积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)设![]() ,求函数
,求函数![]() 的单调增区间;
的单调增区间;
(2)设![]() ,求证:存在唯一的
,求证:存在唯一的![]() ,使得函数
,使得函数![]() 的图象在点
的图象在点![]() 处的切线l与函数
处的切线l与函数![]() 的图象也相切;
的图象也相切;
(3)求证:对任意给定的正数a,总存在正数x,使得不等式![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
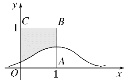
【题目】设X~N(1,σ2),其正态分布密度曲线如图所示,且P(X≥3)=0.0228,那么向正方形OABC中随机投掷10000个点,则落入阴影部分的点的个数的估计值为( )
(附:随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ<ξ<μ+σ)=68.26%,P(μ-2σ<ξ<μ+2σ)=95.44%)
A. 6038 B. 6587 C. 7028 D. 7539
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋内有![]() 个不同的红球,
个不同的红球,![]() 个不同的白球,
个不同的白球,
(1)从中任取![]() 个球,红球的个数不比白球少的取法有多少种?
个球,红球的个数不比白球少的取法有多少种?
(2)若取一个红球记![]() 分,取一个白球记
分,取一个白球记![]() 分,从中任取
分,从中任取![]() 个球,使总分不少于
个球,使总分不少于![]() 分的取法有多少种?
分的取法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
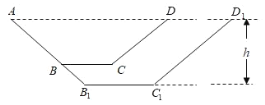
【题目】某农场灌溉水渠长为1000米,横截面是等腰梯形,如图,在等腰梯形![]() 中,
中,![]() ,
,![]() ,其中渠底
,其中渠底![]() 宽为1米,渠口
宽为1米,渠口![]() 宽为3米,渠深
宽为3米,渠深![]() 米.根据国家对农田建设补贴的政策,该农场计划在原水渠的基础上分别沿射线
米.根据国家对农田建设补贴的政策,该农场计划在原水渠的基础上分别沿射线![]() 方向加宽、
方向加宽、![]() 方向加深,若扩建后的水渠横截面
方向加深,若扩建后的水渠横截面![]() 仍是等腰梯形,且面积是原面积的2倍.设扩建后渠深为
仍是等腰梯形,且面积是原面积的2倍.设扩建后渠深为![]() 米,若挖掘费用为每立方米
米,若挖掘费用为每立方米![]() 万元,水渠的内壁(渠底和梯形两腰,
万元,水渠的内壁(渠底和梯形两腰,![]() 端也要重新铺设)铺设混凝土的费用为每平方米
端也要重新铺设)铺设混凝土的费用为每平方米![]() 万元.
万元.
(1)用![]() 表示渠底
表示渠底![]() 的长度,并求出
的长度,并求出![]() 的取值范围;
的取值范围;
(2)问渠深![]() 为多少米时,建设费用最低?
为多少米时,建设费用最低?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com