
【题目】已知函数![]() .
.
(1)设![]() ,求函数
,求函数![]() 的单调增区间;
的单调增区间;
(2)设![]() ,求证:存在唯一的
,求证:存在唯一的![]() ,使得函数
,使得函数![]() 的图象在点
的图象在点![]() 处的切线l与函数
处的切线l与函数![]() 的图象也相切;
的图象也相切;
(3)求证:对任意给定的正数a,总存在正数x,使得不等式![]() 成立.
成立.
【答案】(1)![]() 的单调增区间为(0,
的单调增区间为(0,![]() ];(2)证明见解析;(3)证明见解析.
];(2)证明见解析;(3)证明见解析.
【解析】
(1)求出导函数![]() ,在函数定义域内由
,在函数定义域内由![]() 确定其增区间;
确定其增区间;
(2)先求出![]() 在
在![]() 处的切线方程,设这条切线与
处的切线方程,设这条切线与![]() 的图象切于点
的图象切于点![]() ,由
,由![]() ,得出关于
,得出关于![]() 的方程,然后证明此方程的解在
的方程,然后证明此方程的解在![]() 上存在且唯一.
上存在且唯一.
(3)把问题转化为![]() 在
在![]() 上有解,令
上有解,令![]() ,则只要
,则只要![]() 即可.
即可.
(1)h(x)=g(x)﹣x2=lnx﹣x2,x∈(0,+∞).
令 ,
,
解得![]() .
.
∴函数h(x)的单调增区间为(0,![]() ].
].
(2)证明:设x0>1,![]() ,可得切线斜率
,可得切线斜率![]() ,
,
切线方程为:![]() .
.
假设此切线与曲线y=f(x)=ex相切于点B(x1,![]() ),f′(x)=ex.
),f′(x)=ex.
则k=![]() ,
,
∴![]() .
.
化为:x0lnx0﹣lnx0﹣x0-1=0,x0>1.
下面证明此方程在(1,+∞)上存在唯一解.
令u(x0)=x0lnx0﹣lnx0﹣x0-1,x0>1.
![]() ,在x0∈(1,+∞)上单调递增.
,在x0∈(1,+∞)上单调递增.
又u′(1)=-1,![]() ,
,
∴![]() 在
在![]() 上有唯一实数解
上有唯一实数解![]() ,
,
![]() ,
,![]() ,
,![]() 递减,
递减,
![]() 时,
时,![]() ,
,![]() 递增,
递增,
而![]() ,∴
,∴![]() 在
在![]() 上无解,
上无解,
而![]() ,∴
,∴![]() 在
在![]() 上有唯一解.
上有唯一解.
∴方程![]() 在(1,+∞)上存在唯一解.
在(1,+∞)上存在唯一解.
即:存在唯一的x0,使得函数y=g(x)的图象在点A(x0,g(x0))处的切线l与函数y=f(x)的图象也相切.
(3)证明:![]() ,
,
令v(x)=ex﹣x﹣1,x>0.
∴v′(x)=ex﹣1>0,
∴函数v(x)在x∈(0,+∞)上单调递增,
∴v(x)>v(0)=0.
∴![]() ,
,
∴不等式![]() ,a>0ex﹣x﹣1﹣ax<0,
,a>0ex﹣x﹣1﹣ax<0,
即H(x)=ex﹣x﹣1﹣ax<0,
由对任意给定的正数a,总存在正数x,使得不等式![]() 成立H(x)min<0.
成立H(x)min<0.
H(x)=ex﹣x﹣1﹣ax,a,x∈(0,+∞).
H′(x)=ex﹣1﹣a,令ex﹣1﹣a=0,
解得x=![]() >0,
>0,
函数H(x)在区间(0,![]() )上单调递减,在区间(
)上单调递减,在区间(![]() ,+∞)上单调递增.
,+∞)上单调递增.
∵H(0)=0,∴![]() .
.
∴存在对任意给定的正数a,总存在正数x,使得不等式![]() 成立.
成立.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知直线 (
(![]() 为参数),曲线
为参数),曲线![]() (
(![]() 为参数).
为参数).
(1)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(2)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设点
,设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最大时,点P的坐标.
的距离的最大时,点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年的![]() 月
月![]() 日是全国爱牙日,为了迎接这一节日,某地区卫生部门成立了调查小组,调查“常吃零食与患龋齿的关系”,对该地区小学六年级
日是全国爱牙日,为了迎接这一节日,某地区卫生部门成立了调查小组,调查“常吃零食与患龋齿的关系”,对该地区小学六年级![]() 名学生进行检查,按患龋齿的不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有
名学生进行检查,按患龋齿的不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有![]() 名,常吃零食但不患龋齿的学生有
名,常吃零食但不患龋齿的学生有![]() 名,不常吃零食但患齲齿的学生有
名,不常吃零食但患齲齿的学生有![]() 名.
名.
(1)完成答卷中的![]() 列联表,问:能否在犯错率不超过
列联表,问:能否在犯错率不超过![]() 的前提下,认为该地区学生的常吃零食与患龋齿有关系?
的前提下,认为该地区学生的常吃零食与患龋齿有关系?
(2)![]() 名区卫生部门的工作人员随机分成两组,每组
名区卫生部门的工作人员随机分成两组,每组![]() 人,一组负责数据收集,另一组负责数据处理,求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
人,一组负责数据收集,另一组负责数据处理,求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
附: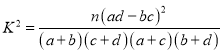
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知圆
中,已知圆![]() 圆心为
圆心为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线与圆
的直线与圆![]() 相交于不同的两点
相交于不同的两点![]() 、
、![]() .
.
(![]() )求
)求![]() 的取值范围;
的取值范围;
(![]() )是否存在常数
)是否存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求
共线?如果存在,求![]() 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为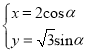 (
(![]() 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线![]() 上的点按坐标变换
上的点按坐标变换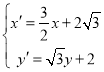 得到曲线
得到曲线![]() ,以原点为极点、
,以原点为极点、![]() 轴的正半轴为极轴,建立极坐标系.
轴的正半轴为极轴,建立极坐标系.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与曲线
两点,与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,如果存在非零常数
,如果存在非零常数![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 是“似周期函数”,非零常数
是“似周期函数”,非零常数![]() 为函数
为函数![]() 的“似周期”.现有下面四个关于“似周期函数”的命题:
的“似周期”.现有下面四个关于“似周期函数”的命题:
①如果“似周期函数”![]() 的“似周期”为
的“似周期”为![]() ,那么它是周期为2的周期函数;
,那么它是周期为2的周期函数;
②函数![]() 是“似周期函数”;
是“似周期函数”;
③如果函数![]() 是“似周期函数”,那么“
是“似周期函数”,那么“![]() 或
或![]() ”.
”.
以上正确结论的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 中点.
中点.
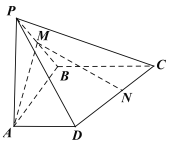
(1)已知点![]() 在棱
在棱![]() 上,且平面
上,且平面![]() 平面
平面![]() ,试确定点
,试确定点![]() 的位置并说明理由;
的位置并说明理由;
(2)设点![]() 是线段
是线段![]() 上的动点,当点
上的动点,当点![]() 在何处时,直线
在何处时,直线![]() 与平面
与平面![]() 所成角最大?并求最大角的正弦值.
所成角最大?并求最大角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com