Question

【题目】已知直线l：和椭圆：相交于点，

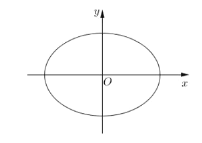
（1）当直线l过椭圆的左焦点和上顶点时，求直线l的方程

（2）点在上，若，求面积的最大值：

（3）如果原点O到直线l的距离是，证明：为直角三角形.

Answer 1

【答案】（1） （2） （3）证明见解析

【解析】

（1）由椭圆方程得左焦点和上顶点坐标，代入直线方程可得结果；

（2）联立直线与椭圆方程可得的坐标，可得弦长，求出点到直线的距离。利用三角形面积公式可得面积，然后利用基本不等式可得最大值；

（3）利用原点O到直线l的距离是可得，联立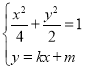，利用韦达定理可得，，求出，利用可证结论.

（1）由知，，，所以，所以，

所以左焦点为，上顶点为，

所以，，所以直线l的方程为.

（2）联立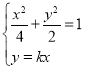，可得或，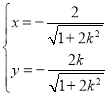

所以，，

所以，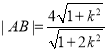

又点到直线的距离，

所以三角形的面积

，

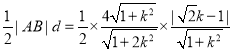
因为要求面积的最大值，所以，

所以，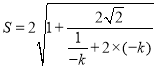

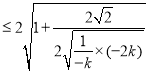
当且仅当时，等号成立.

所以面积的最大值为.

（3）原点到直线的距离为，

所以，

联立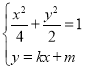，消去并整理得，

由韦达定理得，，

所以，

所以

所以，所以为直角三角形.