
【题目】某大型工厂招聘到一大批新员工.为了解员工对工作的熟练程度,从中随机抽取100人组成样本,统计他们每天加工的零件数,得到如下数据:

将频率作为概率,解答下列问题:
(1)当![]() 时,从全体新员工中抽取2名,求其中恰有1名日加工零件数达到240及以上的概率;
时,从全体新员工中抽取2名,求其中恰有1名日加工零件数达到240及以上的概率;
(2)若根据上表得到以下频率分布直方图,估计全体新员工每天加工零件数的平均数为222个,求![]() 的值(每组数据以中点值代替);
的值(每组数据以中点值代替);
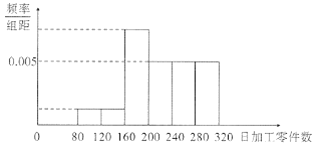
(3)在(2)的条件下,工厂按工作熟练度将新员工分为三个等级:日加工零件数未达200的员工为C级;达到200但未达280的员工为B级;其他员工为A级.工厂打算将样本中的员工编入三个培训班进行全员培训:A,B,C三个等级的员工分别参加高级、中级、初级培训班,预计培训后高级、中级、初级培训班的员工每人的日加工零件数分别可以增加20,30,50.现从样本中随机抽取1人,其培训后日加工零件数增加量为X,求随机变量X的分布列和期望.
【答案】(1)0.42;(2)![]() ;(3)
;(3)![]()
【解析】
(1)先求得![]() 的值,然后求得员工日加工零件数达到
的值,然后求得员工日加工零件数达到![]() 及以上的频率,根据二项分布概率计算公式,计算出所求概率.
及以上的频率,根据二项分布概率计算公式,计算出所求概率.
(2)先求得![]() 的值,然后根据平均数的估计值列方程,求得
的值,然后根据平均数的估计值列方程,求得![]() 的值,进而求得
的值,进而求得![]() 的值.
的值.
(3)![]() 的可能取值为
的可能取值为![]() ,列出分布列并求得数学期望.
,列出分布列并求得数学期望.
(1)依题意![]() ,故员工日加工零件数达到
,故员工日加工零件数达到![]() 及以上的频率为
及以上的频率为![]() ,所以相应的概率可视为
,所以相应的概率可视为![]() ,设抽取的
,设抽取的![]() 名员工中,加工零件数达到
名员工中,加工零件数达到![]() 及以上的人数为
及以上的人数为![]() ,则
,则![]() ,故所求概率为
,故所求概率为![]() .
.
(2)根据后三组数据对应频率分布直方图的纵坐标为![]() ,可知
,可知![]() ,解得
,解得![]() ,因此
,因此![]() ,故根据频率分布直方图得到的样本平均数估计值为
,故根据频率分布直方图得到的样本平均数估计值为![]() ,解得
,解得![]() ,进而
,进而![]() ,故
,故![]() .
.
(3)由已知可得![]() 的可能取值为20,30,50,
的可能取值为20,30,50,
且![]() ,所以
,所以![]() 的分布列为
的分布列为
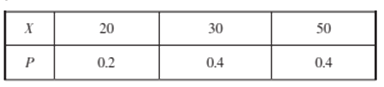
所以![]() .
.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】两圆![]() (
(![]() 圆心,半径
圆心,半径![]() ),与
),与![]() (圆心
(圆心![]() ,半径
,半径![]() )不是同心圆,方程相减(消去二次项)得到的直线
)不是同心圆,方程相减(消去二次项)得到的直线![]() 叫做圆
叫做圆![]() 与圆
与圆![]() 的根轴;
的根轴;
(1)求证:当![]() 与
与![]() 相交于A,B两点时,
相交于A,B两点时,![]() 所在直线为根轴
所在直线为根轴![]() ;
;
(2)对根轴上任意点P,求证:![]() ;
;
(3)设根轴![]() 与
与![]() 交于点H,
交于点H,![]() ,求证:H分
,求证:H分![]() 的比
的比![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() ),以椭圆内一点
),以椭圆内一点![]() 为中点作弦
为中点作弦![]() ,设线段
,设线段![]() 的中垂线与椭圆相交于
的中垂线与椭圆相交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆的离心率;
(Ⅱ)试判断是否存在这样的![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() ,
, ![]() 在同一个圆上,并说明理由.
在同一个圆上,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确命题的个数是( )
①若2b=a+c,则a,b,c成等差数列;
②“a,b,c成等比数列”的充要条件是“b2=ac”;
③若数列{an2}是等比数列,则数列{an}也是等比数列;
④若![]() ,则
,则![]()
A.3B.2C.1D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直角坐标系xOy中,点A坐标为(2,0),点B坐标为(4,3),点C坐标为(1,3),且![]() (t∈R).
(t∈R).
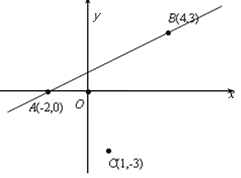
(1) 若CM⊥AB,求t的值;
(2) 当0≤ t ≤1时,求直线CM的斜率k和倾斜角θ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() 与向量
与向量![]() 的对应关系用
的对应关系用![]() 表示.
表示.
(1) 证明:对于任意向量![]() 、
、![]() 及常数m、n,恒有
及常数m、n,恒有![]() ;
;
(2) 证明:对于任意向量![]() ,
,![]() ;
;
(3) 证明:对于任意向量![]() 、
、![]() ,若
,若![]() ,则
,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
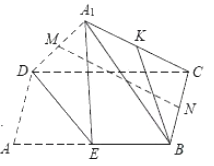
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 的中点,沿
的中点,沿![]() 将
将![]() 折起,点
折起,点![]() 折至
折至![]() 处(
处(![]() 与
与![]() 不重合),若
不重合),若![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 的中点,则在
的中点,则在![]() 折起过程中( )
折起过程中( )
A.![]() 可以与
可以与![]() 垂直
垂直
B.不能同时做到![]() 平面
平面![]() 且
且![]() 平面
平面![]()
C.当![]() 时,
时,![]() 平面
平面![]()
D.直线![]() 、
、![]() 与平面
与平面![]() 所成角分别为
所成角分别为![]() 、
、![]() ,
,![]() 、
、![]() 能够同时取得最大值
能够同时取得最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),且曲线
为参数),且曲线![]() 上的点
上的点![]() 对应的参数
对应的参数![]() ,以
,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)若曲线![]() 上的
上的![]() 两点满足
两点满足![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,求证:点
,求证:点![]() 在以
在以![]() 为圆心的定圆上.
为圆心的定圆上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com