
【题目】在平行四边形ABCD中,AB=1,AD![]() ,且∠BAD=45°,以BD为折线,把△ABD折起,使AB⊥DC,连接AC,得到三棱锥A﹣BCD.
,且∠BAD=45°,以BD为折线,把△ABD折起,使AB⊥DC,连接AC,得到三棱锥A﹣BCD.
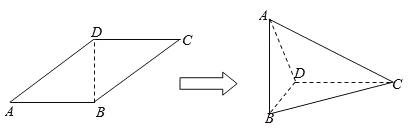
(1)求证:平面ABD⊥平面BCD;
(2)求二面角B﹣AC﹣D的大小.
【答案】(1)证明见解析;(2)60°.
【解析】
(1)通过证明AB⊥平面BCD,得面面垂直;
(2)取BC中点E,过点E作EF⊥AC交AC于点F,连接DE,DF,EF,证明∠DFE为所求二面角,即可计算求解.
(1)证明:∵AB=1,AD![]() ,且∠BAD=45°,
,且∠BAD=45°,
∴BD=1,则AD2=AB2+BD2,即AB⊥BD,
又AB⊥DC,BD∩DC=D,且都在平面BCD内,
∴AB⊥平面BCD,
∵AB在平面ABD内,
∴平面ABD⊥平面BCD;

(2)取BC中点E,过点E作EF⊥AC交AC于点F,连接DE,DF,EF,
∵BD=CD=1,
∴DE⊥BC,
∵AB⊥平面BCD,DE平面BCD,
∴AB⊥DE,
∵AB∩BC=B,且都在平面ABC内,
∴DE⊥平面ABC,
∵AC平面ABC,
∴AC⊥DE,
又EF⊥AC,DE∩EF=E,且都在平面DEF内,
∴AC⊥平面DEF,
∴∠DFE为所求二面角,
在Rt△DEF中,∠DEF=90°,![]() ,
,![]() ,
,
∴ ,
,
∴∠DFE=60°,即二面角B﹣AC﹣D的大小为60°.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系xOy中,曲线C1的普通方程为![]() ,曲线C2参数方程为
,曲线C2参数方程为![]() 为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,直线l的极坐标方程为
为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,直线l的极坐标方程为![]() .
.
(1)求C1的参数方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知P是C2上参数![]() 对应的点,Q为C1上的点,求PQ中点M到直线
对应的点,Q为C1上的点,求PQ中点M到直线![]() 的距离取得最大值时,点Q的直角坐标.
的距离取得最大值时,点Q的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,(其中
,(其中![]() 是自然对数的底数).
是自然对数的底数).
(1)若![]() ,求函数
,求函数![]() 在
在![]() 上的最大值.
上的最大值.
(2)若![]() ,关于x的方程
,关于x的方程![]() 有且仅有一个根,求实数k的取值范围.
有且仅有一个根,求实数k的取值范围.
(3)若对任意的![]() 、
、![]() ,
,![]() ,不等式
,不等式![]() 都成立,求实数a的取值范围.
都成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学家欧拉在1765年提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线被后人称之为三角形的欧拉线.已知△ABC的顶点A(2,0),B(0,4),且AC=BC,则△ABC的欧拉线的方程为( )
A.x+2y+3=0B.2x+y+3=0C.x﹣2y+3=0D.2x﹣y+3=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() ,
,![]() 为线段
为线段![]() 的中点(如图1).将
的中点(如图1).将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,
,![]() 为线段
为线段![]() 的中点(如图2).
的中点(如图2).
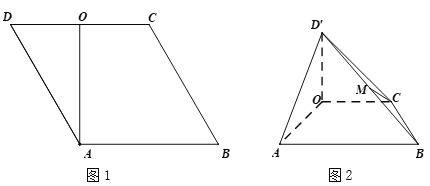
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)当四棱锥![]() 的体积为
的体积为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】矩形ABCD中,![]() ,沿对角线AC将三角形ADC折起,得到四面体
,沿对角线AC将三角形ADC折起,得到四面体![]() ,四面体
,四面体![]() 外接球表面积为
外接球表面积为![]() ,当四面体
,当四面体![]() 的体积取最大值时,四面体
的体积取最大值时,四面体![]() 的表面积为( )
的表面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为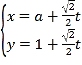 (
(![]() 为参数,
为参数,![]() ).以
).以![]() 为极点,
为极点,![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com