
【题目】对于函数![]() ,若存在区间
,若存在区间![]() ,使得
,使得![]() ,则称函数
,则称函数![]() 为“可等域函数”,区间
为“可等域函数”,区间![]() 为函数的一个“可等域区间”.给出下列四个函数:
为函数的一个“可等域区间”.给出下列四个函数:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() .
.
其中存在唯一“可等域区间”的“可等域函数”的序号是________.
【答案】②③
【解析】
根据存在区间![]() ,使得
,使得![]() ,则称函数
,则称函数![]() 为“可等域函数”,区间
为“可等域函数”,区间![]() 为函数的一个“可等域区间”,对四个函数逐一判断,即可得到答案.
为函数的一个“可等域区间”,对四个函数逐一判断,即可得到答案.
对于①,![]() 是
是![]() 的可等域区间,但不唯一,故①不成立;
的可等域区间,但不唯一,故①不成立;
对于②,![]() ,且
,且![]() 在
在![]() 时递减,在
时递减,在![]() 时递增,
时递增,
若![]() ,则
,则![]() ,故
,故![]()
又![]() ,
,![]() ,而
,而![]() ,故
,故![]() ,故
,故![]() 是一个可等域区间;
是一个可等域区间;
若![]() ,则
,则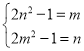 ,解得
,解得![]() ,
,![]() ,不合题意,
,不合题意,
若![]() ,则
,则![]() 有两个非负解,但此方程的两解为
有两个非负解,但此方程的两解为![]() 和
和![]() ,也不合题意,
,也不合题意,
![]() 函数
函数![]() 只有一个等可域区间
只有一个等可域区间![]() ,故②成立;
,故②成立;
对于③,函数![]() 的值域是
的值域是![]() ,
,
![]()
![]() ,函数
,函数![]() 在
在![]() 上是增函数,
上是增函数,
考察方程![]() ,由于函数
,由于函数![]() 与
与![]() 只有两个交点
只有两个交点![]() ,
,![]() ,
,
即方程![]() 只有两个解
只有两个解![]() 和
和![]() ,
,
![]() 此函数只有一个等可域区间
此函数只有一个等可域区间![]() ,故③成立;
,故③成立;
对于④,函数![]() 在定义域
在定义域![]() 上是增函数,
上是增函数,
若函数![]() 有等可域区间
有等可域区间![]() ,则
,则![]() ,
,![]() ,
,
但方程![]() 无解,故此函数无可等域区间,故④不成立.
无解,故此函数无可等域区间,故④不成立.
综上所述,只有②③正确.
故答案为:②③.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】根据如图给出的2005年至2016年我国人口总量及增长率的统计图,以下结论不正确的是![]()
![]()
A. 自2005年以来,我国人口总量呈不断增加趋势
B. 自2005年以来,我国人口增长率维持在![]() 上下波动
上下波动
C. 从2005年后逐年比较,我国人口增长率在2016年增长幅度最大
D. 可以肯定,在2015年以后,我国人口增长率将逐年变大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为![]() (α为参数),在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,点P的极坐标为
(α为参数),在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,点P的极坐标为![]() ,直线l的极坐标方程为
,直线l的极坐标方程为![]() .
.
(1)求直线l的直角坐标方程与曲线C的普通方程;
(2)若Q是曲线C上的动点,M为线段PQ的中点,直线l上有两点A,B,始终满足|AB|=4,求△MAB面积的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,已知棱
中,已知棱![]() ,
,![]() ,
,![]() 两两垂直,长度分别为1,2,2.若
两两垂直,长度分别为1,2,2.若![]() (
(![]() ),且向量
),且向量![]() 与
与![]() 夹角的余弦值为
夹角的余弦值为![]() .
.
(1)求![]() 的值;
的值;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若椭圆![]() 的焦点在x轴上,离心率为
的焦点在x轴上,离心率为![]() ,依次连接
,依次连接![]() 的四个顶点所得四边形的面积为40.
的四个顶点所得四边形的面积为40.
(1)试求![]() 的标准方程;
的标准方程;
(2)若曲线M上任意一点到![]() 的右焦点的距离与它到直线
的右焦点的距离与它到直线![]() 的距离相等,直线
的距离相等,直线![]() 经过
经过![]() 的下顶点和右顶点,
的下顶点和右顶点,![]() ,直线
,直线![]() 与曲线M相交于点P、Q(点P在第一象限内,点Q在第四象限内),设
与曲线M相交于点P、Q(点P在第一象限内,点Q在第四象限内),设![]() 的下顶点是B,上顶点是D,且
的下顶点是B,上顶点是D,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
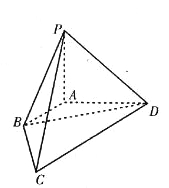
【题目】某学习小组在研究性学习中,对昼夜温差大小与绿豆种子一天内出芽数之间的关系进行研究该小组在4月份记录了1日至6日每天昼夜最高、最低温度(如图1),以及浸泡的100颗绿豆种子当天内的出芽数(如图2).
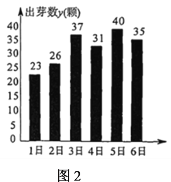
根据上述数据作出散点图,可知绿豆种子出芽数(颗)和温差具有线性相关关系.
附: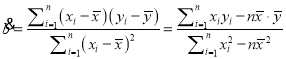 ,
,![]()
(1)求绿豆种子出芽数(颗)关于温差的回归方程;
(2)假如4月1日至7日的日温差的平均值为11℃,估计4月7日浸泡的10000颗绿豆种子一天内的出芽数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com