
【题目】如图,在平面直角坐标系xOy中,已知椭圆 ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,C为椭圆上位于第一象限内的一点.
,C为椭圆上位于第一象限内的一点.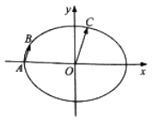
(1)若点C的坐标为(2, ![]() ),求a,b的值;
),求a,b的值;
(2)设A为椭圆的左顶点,B为椭圆上一点,且 ![]() =
= ![]()
![]() ,求直线AB的斜率.
,求直线AB的斜率.
【答案】
(1)
解:由题意可知:椭圆的离心率e= ![]() =
= ![]() =
= ![]() ,则
,则 ![]() =
= ![]() ,①
,①
由点C在椭圆上,将(2, ![]() )代入椭圆方程,
)代入椭圆方程, ![]() ,②
,②
解得:a2=9,b2=5,
∴a=3,b= ![]() ,
,
(2)
解:方法一:由(1)可知: ![]() =
= ![]() ,则椭圆方程:5x2+9y2=5a2,
,则椭圆方程:5x2+9y2=5a2,
设直线OC的方程为x=my(m>0),B(x1,y1),C(x2,y2),
![]() ,消去x整理得:5m2y2+9y2=5a2,
,消去x整理得:5m2y2+9y2=5a2,
∴y2= ![]() ,由y2>0,则y2=
,由y2>0,则y2= ![]() ,
,
由 ![]() =
= ![]()
![]() ,则AB∥OC,设直线AB的方程为x=my﹣a,
,则AB∥OC,设直线AB的方程为x=my﹣a,
则 ![]() ,整理得:(5m2+9)y2﹣10amy=0,
,整理得:(5m2+9)y2﹣10amy=0,
由y=0,或y1= ![]() ,
,
由 ![]() =
= ![]()
![]() ,则(x1+a,y1)=(
,则(x1+a,y1)=( ![]() x2,
x2, ![]() y2),
y2),
则y2=2y1,
则 ![]() =2×
=2× ![]() ,(m>0),
,(m>0),
解得:m= ![]() ,
,
则直线AB的斜率 ![]() =
= ![]() ;
;
方法二:由(1)可知:椭圆方程5x2+9y2=5a2,则A(﹣a,0),
B(x1,y1),C(x2,y2),
由 ![]() =
= ![]()
![]() ,则(x1+a,y1)=(
,则(x1+a,y1)=( ![]() x2,vy2),则y2=2y1,
x2,vy2),则y2=2y1,
由B,C在椭圆上,
∴  ,解得:
,解得: 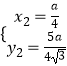 ,
,
则直线直线AB的斜率k= ![]() =
= ![]() .
.
直线AB的斜率 ![]()
【解析】(1)利用抛物线的离心率求得 ![]() =
= ![]() ,将(2,
,将(2, ![]() )代入椭圆方程,即可求得a和b的值;(2)方法二:设直线OC的斜率,代入椭圆方程,求得C的纵坐标,则直线直线AB的方程为x=my﹣a,代入椭圆方程,求得B的纵坐标,由
)代入椭圆方程,即可求得a和b的值;(2)方法二:设直线OC的斜率,代入椭圆方程,求得C的纵坐标,则直线直线AB的方程为x=my﹣a,代入椭圆方程,求得B的纵坐标,由 ![]() =
= ![]()
![]() ,则直线直线AB的斜率k=
,则直线直线AB的斜率k= ![]() =
= ![]() ;方法二:由
;方法二:由 ![]() =
= ![]()
![]() ,y2=2y1 , 将B和C代入椭圆方程,即可求得C点坐标,利用直线的离心率公式即可求得直线AB的斜率.
,y2=2y1 , 将B和C代入椭圆方程,即可求得C点坐标,利用直线的离心率公式即可求得直线AB的斜率.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】去年“十一”期间,昆曲高速公路车辆较多.某调查公司在曲靖收费站从7座以下小型汽车中按进收费站的先后顺序,每间隔50辆就抽取一辆的抽样方法抽取40辆汽车进行抽样调查,将他们在某段高速公路的车速(![]() )分成六段:
)分成六段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 后,得到如图的频率分布直方图.
后,得到如图的频率分布直方图.
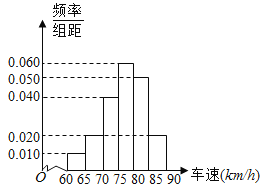
(I)调查公司在抽样时用到的是哪种抽样方法?
(II)求这40辆小型汽车车速的众数和中位数的估计值;
(III)若从这40辆车速在![]() 的小型汽车中任意抽取2辆,求抽出的2辆车车速都在
的小型汽车中任意抽取2辆,求抽出的2辆车车速都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究小组欲研究昼夜温差大小与患感冒人数之间的关系,统计得到1至6月份每月9号的昼夜温差![]() 与因患感冒而就诊的人数
与因患感冒而就诊的人数![]() 的数据,如下表:
的数据,如下表:
日期 | 1月9号 | 2月9号 | 3月9号 | 4月9号 | 5月9号 | 6月9号 |
| 10 | 11 | 13 | 12 | 8 | 6 |
| 22 | 25 | 29 | 26 | 16 | 12 |
该研究小组的研究方案是:先从这6组数据中选取2组,用剩下的4组数据求回归方程,再用之前被选取的2组数据进行检验.
(1)若选取1月和6月的数据作为检验数据,请根据剩下的2至5月的数据,求出![]() 关于
关于![]() 的线性回归方程;(计算结果保留最简分数)
的线性回归方程;(计算结果保留最简分数)
(2)若用(1)中所求的回归方程作预报,得到的估计数据与所选出的检验数据的误差不超过2人,则认为得到的回归方程是理想的,试问该研究小组所得回归方程是否理想?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的长轴长为6,离心率为 ![]() ,F2为椭圆的右焦点.
,F2为椭圆的右焦点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)点M在圆x2+y2=8上,且M在第一象限,过M作圆x2+y2=8的切线交椭圆于P,Q两点,判断△PF2Q的周长是否为定值并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,g(x)=lnx,其中e为自然对数的底数.
,g(x)=lnx,其中e为自然对数的底数.
(1)求函数y=f(x)g(x)在x=1处的切线方程;
(2)若存在x1 , x2(x1≠x2),使得g(x1)﹣g(x2)=λ[f(x2)﹣f(x1)]成立,其中λ为常数,求证:λ>e;
(3)若对任意的x∈(0,1],不等式f(x)g(x)≤a(x﹣1)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=asinωx+bcosωx(0<ω<5,ab≠0)的图象的一条对称轴方程是 ![]() ,函数f'(x)的图象的一个对称中心是
,函数f'(x)的图象的一个对称中心是 ![]() ,则f(x)的最小正周期是( )
,则f(x)的最小正周期是( )
A.![]()
B.![]()
C.π
D.2π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)全网传播的融合指数是衡量电视媒体在中国网民中影响了的综合指标.根据相关报道提供的全网传播2015年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.
组号 | 分组 | 频数 |
1 |
| 2 |
2 |
| 8 |
3 |
| 7 |
4 |
| 3 |
(Ⅰ)现从融合指数在![]() 和
和![]() 内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在
内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在![]() 的概率;
的概率;
(Ⅱ)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com