[题目]如图.设Ox.Oy是平面内相交成45°角的两条数轴. . 分别是x轴.y轴正方向同向的单位向量.若向量 =x +y .则把有序数对(x.y)叫做向量在坐标系xOy中的坐标.在此坐标系下.假设 =(﹣2.2 ). =(2.0). =(5.﹣3 ).则下列命题不正确的是( ) A. =(1.0)B.| |=2 C. ∥ D. ⊥ 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】如图，设Ox、Oy是平面内相交成45°角的两条数轴，、分别是x轴、y轴正方向同向的单位向量，若向量 =x +y ，则把有序数对（x，y）叫做向量在坐标系xOy中的坐标，在此坐标系下，假设 =（﹣2，2 ）， =（2，0）， =（5，﹣3 ），则下列命题不正确的是（）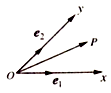
A. =（1，0）
B.| |=2
C. ∥
D. ⊥

【答案】B
【解析】解： =1× +0× ，∴ =（1，0）；故A正确；由余弦定理可知| |= =2，故B错误；
∵ = =（3，﹣3 ）=﹣ ，∴ ∥ ，故C正确；
的直角坐标为（0，2），的直角坐标系为（2，0），
∴ ．故D正确．
故选B．
利用定义判断A，根据余弦定理判断B，根据向量共线定理判定C，转化为正交分解判断D．

练习册系列答案

新课程寒假作业本山西教育出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知不等式组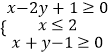表示的平面区域为D，则
（1）z=x2+y2的最小值为．
（2）若函数y=|2x﹣1|+m的图象上存在区域D上的点，则实数m的取值范围是．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）的定义域是D，若存在常数m、M，使得m≤f（x）≤M对任意x∈D成立，则称函数f（x）是D上的有界函数，其中m称为函数f（x）的下界，M称为函数f（x）的上界；特别地，若“=”成立，则m称为函数f（x）的下确界，M称为函数f（x）的上确界．（Ⅰ）判断是否是有界函数？说明理由；
（Ⅱ）若函数f（x）=1+a2x+4x（x∈（﹣∞，0））是以﹣3为下界、3为上界的有界函数，求实数a的取值范围；
（Ⅲ）若函数，T（a）是f（x）的上确界，求T（a）的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数 ,其中 (为自然对数的底数).

（Ⅰ）讨论函数的单调性,并写出相应的单调区间；

（Ⅱ）设,若函数对任意都成立,求的最大值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】定义在R上的单调函数f（x）满足：f（x+y）=f（x）+f（y），若F（x）=f（asinx）+f（sinx+cos2x﹣3）在（0，π）上有零点，则a的取值范围是．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某商场柜台销售某种产品，每件产品的成本为10元，并且每件产品需向该商场交a元（3≤a≤7）的管理费，预计当每件产品的售价为x元（20≤x≤25）时，一天的销售量为（x﹣30）2件．（Ⅰ）求该柜台一天的利润f（x）（元）与每件产品的售价x的函数关系式；
（Ⅱ）当每件产品的售价为多少元时，该柜台一天的利润f（x）最大，并求出f（x）的最大值g（a）．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）= cos（2x﹣ ）．
（1）若sinθ=﹣ ，θ∈（，2π），求f（θ+ ）的值；
（2）若x∈[ ， ]，求函数f（x）的单调减区间．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知对任意平面向量 =（x，y），把绕其起点沿逆时针方向旋转θ角得到的向量 =（xcosθ﹣ysinθ，xsinθ+ycosθ），叫做把点B绕点A逆时针方向旋转θ得到点P．
（1）已知平面内点A（2，3），点B（2+2 ，1）．把点B绕点A逆时针方向旋转角得到点P，求点P的坐标．
（2）设平面内曲线C上的每一点绕坐标原点沿顺时针方向旋转后得到的点的轨迹方程是曲线y= ，求原来曲线C的方程．