
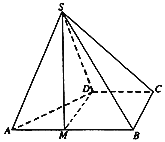
ЁОЬтФПЁПЫФРтзЖSЃABCDЕФЕзУцABCDЮЊжБНЧЬнаЮЃЌABЁЮCDЃЌABЁЭBCЃЌABЃН2BCЃН2CDЃН2ЃЌЁїSADЮЊе§Ш§НЧаЮЃЎ
ЃЈЂёЃЉЕуMЮЊРтABЩЯвЛЕуЃЌШєBCЁЮЦНУцSDMЃЌAMЃНІЫABЃЌЧѓЪЕЪ§ІЫЕФжЕЃЛ
ЃЈЂђЃЉШєBCЁЭSDЃЌЧѓЖўУцНЧAЃSBЃCЕФгрЯвжЕЃЎ
ЁОД№АИЁПЃЈЂёЃЉ![]() ЃЈЂђЃЉ
ЃЈЂђЃЉ![]()
ЁОНтЮіЁП
ЃЈЂёЃЉгЩЯпУцЦНааЕФаджЪЖЈРэПЩЕУ![]() ЃЌОнДЫПЩжЊЫФБпаЮBCDMЮЊЦНааЫФБпаЮЃЌОнДЫПЩЕУ
ЃЌОнДЫПЩжЊЫФБпаЮBCDMЮЊЦНааЫФБпаЮЃЌОнДЫПЩЕУ![]() .
.
ЃЈЂђЃЉгЩМИКЮЙиЯЕЃЌдкЦНУц![]() ФкЙ§Еу
ФкЙ§Еу![]() зї
зї![]() жБЯп
жБЯп![]() гкЕу
гкЕу![]() ЃЌвдЕуEЮЊзјБъдЕуЃЌEAЗНЯђЮЊXжсЃЌECЗНЯђЮЊYжсЃЌESЗНЯђЮЊZжсНЈСЂПеМфзјБъЯЕЃЌОнДЫПЩЕУЦНУц
ЃЌвдЕуEЮЊзјБъдЕуЃЌEAЗНЯђЮЊXжсЃЌECЗНЯђЮЊYжсЃЌESЗНЯђЮЊZжсНЈСЂПеМфзјБъЯЕЃЌОнДЫПЩЕУЦНУц![]() ЕФвЛИіЗЈЯђСП
ЕФвЛИіЗЈЯђСП![]() ЃЌЦНУц
ЃЌЦНУц![]() ЕФвЛИіЗЈЯђСП
ЕФвЛИіЗЈЯђСП![]() ЃЌОнДЫМЦЫуПЩЕУЖўУцНЧ
ЃЌОнДЫМЦЫуПЩЕУЖўУцНЧ![]() грЯвжЕЮЊ
грЯвжЕЮЊ![]() .
.
ЃЈЂёЃЉвђЮЊ![]() ЦНУцSDM,
ЦНУцSDM,![]()
![]() ЦНУцABCD,ЦНУцSDM
ЦНУцABCD,ЦНУцSDM ![]() ЦНУцABCD=DM,Ыљвд
ЦНУцABCD=DM,Ыљвд![]() ЃЌ
ЃЌ
вђЮЊ![]() ,ЫљвдЫФБпаЮBCDMЮЊЦНааЫФБпаЮЃЌгж
,ЫљвдЫФБпаЮBCDMЮЊЦНааЫФБпаЮЃЌгж![]() ,ЫљвдMЮЊABЕФжаЕу.
,ЫљвдMЮЊABЕФжаЕу.
вђЮЊ![]()
![]() .
.

ЃЈЂђЃЉвђЮЊ![]()
![]() ЃЌ
ЃЌ ![]()
![]() ЃЌЫљвд
ЃЌЫљвд![]() ЦНУц
ЦНУц![]() ЃЌгжвђЮЊ
ЃЌгжвђЮЊ![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ
ЫљвдЦНУц![]() ЦНУц
ЦНУц![]() ЃЌЦНУц
ЃЌЦНУц![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ
дкЦНУц![]() ФкЙ§Еу
ФкЙ§Еу![]() зї
зї![]() жБЯп
жБЯп![]() гкЕу
гкЕу![]() ЃЌдђ
ЃЌдђ![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ
дк![]() КЭ
КЭ![]() жаЃЌвђЮЊ
жаЃЌвђЮЊ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌ
ЃЌ
гжгЩЬтжЊ![]() ЃЌЫљвд
ЃЌЫљвд![]() Ыљвд
Ыљвд![]() ЃЌ
ЃЌ
вдЯТНЈЯЕЧѓНт.вдЕуEЮЊзјБъдЕуЃЌEAЗНЯђЮЊXжсЃЌECЗНЯђЮЊYжсЃЌESЗНЯђЮЊZжсНЈСЂШчЭМЫљЪОПеМфзјБъЯЕЃЌ
дђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЩшЦНУц![]() ЕФЗЈЯђСП
ЕФЗЈЯђСП![]() ЃЌдђ
ЃЌдђ ЃЌЫљ
ЃЌЫљ![]() ЃЌ
ЃЌ
Сю![]() ЕУ
ЕУ![]() ЮЊЦНУц
ЮЊЦНУц![]() ЕФвЛИіЗЈЯђСПЃЌ
ЕФвЛИіЗЈЯђСПЃЌ
ЭЌРэЕУ![]() ЮЊЦНУц
ЮЊЦНУц![]() ЕФвЛИіЗЈЯђСПЃЌ
ЕФвЛИіЗЈЯђСПЃЌ
 ЃЌвђЮЊЖўУцНЧ
ЃЌвђЮЊЖўУцНЧ![]() ЮЊЖлНЧ.
ЮЊЖлНЧ.
ЫљвдЖўУцНЧ![]() грЯвжЕЮЊ
грЯвжЕЮЊ![]() .
.
ЁОЕуОІЁП
БОЬтПМВщСЫСЂЬхМИКЮжаЕФХаЖЯЖЈРэКЭЖўУцНЧЕФЧѓНтЮЪЬтЃЌвтдкПМВщбЇЩњЕФПеМфЯыЯѓФмСІКЭТпМЭЦРэФмСІЃЛНтД№БОЬтЙиМќдкгкФмРћгУжБЯпгыжБЯпЁЂжБЯпгыЦНУцЁЂЦНУцгыЦНУцЙиЯЕЕФЯрЛЅзЊЛЏЃЌЭЈЙ§бЯУмЭЦРэЃЌУїШЗНЧЕФЙЙГЩ.ЭЌЪБЖдгкСЂЬхМИКЮжаНЧЕФМЦЫуЮЪЬтЃЌЭљЭљПЩвдРћгУПеМфЯђСПЗЈЃЌЭЈЙ§ЧѓНтЦНУцЕФЗЈЯђСПЃЌРћгУЯђСПЕФМаНЧЙЋЪНЧѓНт.
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
19
ЁОЬтФПЁПаЁУїдкЪЏМвзЏЪаФГЮяСїХЩЫЭЙЋЫОевЕНСЫвЛЗнХЩЫЭдБЕФЙЄзїЃЌИУЙЋЫОИјГіСЫСНжжШеаНаНГъЗНАИЃЎМзЗНАИЃКЕзаН100дЊЃЌУПХЩЫЭвЛЕЅНБРј1дЊЃЛввЗНАИЃКЕзаН140дЊЃЌУПШеЧА55ЕЅУЛгаНБРјЃЌГЌЙ§55ЕЅЕФВПЗжУПЕЅНБРј12дЊЃЎ
ЃЈЂёЃЉЧыЗжБ№ЧѓГіМзЁЂввСНжжаНГъЗНАИжаШеаНyЃЈЕЅЮЛЃКдЊЃЉгыЫЭЛѕЕЅЪ§nЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈЂђЃЉИљОнИУЙЋЫОЫљгаХЩЫЭдБ100ЬьЕФХЩЫЭМЧТМЃЌЗЂЯжХЩЫЭдБЕФШеЦНОљХЩЫЭЕЅЪ§ТњзувдЯТЬѕМўЃКдкет100ЬьжаЕФХЩЫЭСПжИБъТњзуШчЭМЫљЪОЕФжБЗНЭМЃЌЦфжаЕБФГЬьЕФХЩЫЭСПжИБъдкЃЈ![]() ЃЌ
ЃЌ![]() ]ЃЈnЃН1ЃЌ2ЃЌ3ЃЌ4ЃЌ5ЃЉЪБЃЌШеЦНОљХЩЫЭСПЮЊ50ЃЋ2nЕЅЃЎШєНЋЦЕТЪЪгЮЊИХТЪЃЌЛиД№ЯТСаЮЪЬтЃК
]ЃЈnЃН1ЃЌ2ЃЌ3ЃЌ4ЃЌ5ЃЉЪБЃЌШеЦНОљХЩЫЭСПЮЊ50ЃЋ2nЕЅЃЎШєНЋЦЕТЪЪгЮЊИХТЪЃЌЛиД№ЯТСаЮЪЬтЃК
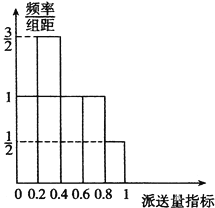
ЂйИљОнвдЩЯЪ§ОнЃЌЩшУПУћХЩЫЭдБЕФШеаНЮЊXЃЈЕЅЮЛЃКдЊЃЉЃЌЪдЗжБ№ЧѓГіМзЁЂввСНжжЗНАИЕФШеаНXЕФЗжВМСаЃЌЪ§бЇЦкЭћМАЗНВюЃЛ
ЂкНсКЯЂйжаЕФЪ§ОнЃЌИљОнЭГМЦбЇЕФЫМЯыЃЌАяжњаЁУїЗжЮіЃЌЫћбЁдёФФжжаНГъЗНАИБШНЯКЯЪЪЃЌВЂЫЕУїФуЕФРэгЩЁЃ
ЃЈВЮПМЪ§ОнЃК0ЃЎ62ЃН0ЃЎ36ЃЌ1ЃЎ42ЃН1ЃЎ9 6ЃЌ2ЃЎ6 2ЃН6ЃЎ76ЃЌ3ЃЎ42ЃН1 1ЃЎ56ЃЌ3ЃЎ62ЃН12ЃЎ96ЃЌ4ЃЎ62ЃН21ЃЎ16ЃЌ15ЃЎ62ЃН243ЃЎ36ЃЌ20ЃЎ42ЃН416ЃЎ16ЃЌ44ЃЎ42ЃН1971ЃЎ36ЃЉ
ЁОД№АИЁПЃЈЂёЃЉМзЗНАИЕФКЏЪ§ЙиЯЕЪНЮЊЃК ![]() ЃЌввЗНАИЕФКЏЪ§ЙиЯЕЪНЮЊЃК
ЃЌввЗНАИЕФКЏЪ§ЙиЯЕЪНЮЊЃК![]() ЃЛЃЈЂђЃЉЂйМћНтЮіЃЌЂкМћНтЮі.
ЃЛЃЈЂђЃЉЂйМћНтЮіЃЌЂкМћНтЮі.
ЁОНтЮіЁП
ЃЈЂёЃЉгЩЬтвтПЩЕУМзЗНАИжаХЩЫЭдБШеаН![]() ЃЈЕЅЮЛЃКдЊЃЉгыЫЭЕЅЪ§
ЃЈЕЅЮЛЃКдЊЃЉгыЫЭЕЅЪ§![]() ЕФКЏЪ§ЙиЯЕЪНЮЊЃК
ЕФКЏЪ§ЙиЯЕЪНЮЊЃК ![]() ЃЌ ввЗНАИжаХЩЫЭдБШеаН
ЃЌ ввЗНАИжаХЩЫЭдБШеаН![]() ЃЈЕЅЮЛЃКдЊЃЉгыЫЭЕЅЪ§
ЃЈЕЅЮЛЃКдЊЃЉгыЫЭЕЅЪ§![]() ЕФКЏЪ§ЙиЯЕЪНЮЊЃК
ЕФКЏЪ§ЙиЯЕЪНЮЊЃК![]() .
.
ЃЈЂђЃЉЂйгЩЬтвтЧѓЕУXЕФЗжВМСаЃЌОнДЫМЦЫуПЩЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.
ЂкД№АИвЛЃКгЩвдЩЯЕФМЦЫуПЩжЊЃЌ![]() дЖаЁгк
дЖаЁгк![]() ЃЌМДМзЗНАИШеЙЄзЪЪеШыВЈЖЏЯрЖдНЯаЁЃЌЫљвдаЁУїгІбЁдёМзЗНАИ.
ЃЌМДМзЗНАИШеЙЄзЪЪеШыВЈЖЏЯрЖдНЯаЁЃЌЫљвдаЁУїгІбЁдёМзЗНАИ.
Д№АИЖўЃКгЩвдЩЯЕФМЦЫуНсЙћПЩвдПДГіЃЌ![]() ЃЌЫљвдаЁУїгІбЁдёввЗНАИ.
ЃЌЫљвдаЁУїгІбЁдёввЗНАИ.
ЃЈЂёЃЉМзЗНАИжаХЩЫЭдБШеаН![]() ЃЈЕЅЮЛЃКдЊЃЉгыЫЭЕЅЪ§
ЃЈЕЅЮЛЃКдЊЃЉгыЫЭЕЅЪ§![]() ЕФКЏЪ§ЙиЯЕЪНЮЊЃК
ЕФКЏЪ§ЙиЯЕЪНЮЊЃК ![]() ЃЌ
ЃЌ
ввЗНАИжаХЩЫЭдБШеаН![]() ЃЈЕЅЮЛЃКдЊЃЉгыЫЭЕЅЪ§
ЃЈЕЅЮЛЃКдЊЃЉгыЫЭЕЅЪ§![]() ЕФКЏЪ§ЙиЯЕЪНЮЊЃК
ЕФКЏЪ§ЙиЯЕЪНЮЊЃК![]()
ЃЈЂђЃЉЂйгЩвбжЊЃЌдкет100ЬьжаЃЌИУЙЋЫОХЩЫЭдБШеЦНОљХЩЫЭЕЅЪ§ТњзуШчЯТБэИёЃК
ЕЅЪ§ | 52 | 54 | 56 | 58 | 60 |
ЦЕТЪ | 0.2 | 0.3 | 0.2 | 0.2 | 0.1 |
Ыљвд![]() ЕФЗжВМСаЮЊЃК
ЕФЗжВМСаЮЊЃК
| 152 | 154 | 156 | 158 | 160 |
| 0.2 | 0.3 | 0.2 | 0.2 | 0.1 |
Ыљвд![]()
![]()
Ыљвд![]() ЕФЗжВМСаЮЊЃК
ЕФЗжВМСаЮЊЃК
| 140 | 152 | 176 | 200 |
| 0.5 | 0.2 | 0.2 | 0.1 |
Ыљвд![]()
![]()
ЂкД№АИвЛЃКгЩвдЩЯЕФМЦЫуПЩжЊЃЌЫфШЛ![]() ЃЌЕЋСНепЯрВюВЛДѓЃЌЧв
ЃЌЕЋСНепЯрВюВЛДѓЃЌЧв![]() дЖаЁгк
дЖаЁгк![]() ЃЌМДМзЗНАИШеЙЄзЪЪеШыВЈЖЏЯрЖдНЯаЁЃЌЫљвдаЁУїгІбЁдёМзЗНАИ.
ЃЌМДМзЗНАИШеЙЄзЪЪеШыВЈЖЏЯрЖдНЯаЁЃЌЫљвдаЁУїгІбЁдёМзЗНАИ.
Д№АИЖўЃКгЩвдЩЯЕФМЦЫуНсЙћПЩвдПДГіЃЌ![]() ЃЌМДМзЗНАИШеЙЄзЪЦкЭћаЁгкввЗНАИШеЙЄзЪЦкЭћЃЌЫљвдаЁУїгІбЁдёввЗНАИ.
ЃЌМДМзЗНАИШеЙЄзЪЦкЭћаЁгкввЗНАИШеЙЄзЪЦкЭћЃЌЫљвдаЁУїгІбЁдёввЗНАИ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2017ФъСНЛсМЬајЙизЂСЫЯчДхНЬЪІЕФЮЪЬт,ЫцзХГЧЯчЗЂеЙЪЇКт,ЯчДхНЬЪІД§гіЕУВЛЕНБЃеЯ,СїЪЇЯжЯѓбЯжи,НЬЪІЖЬШБЛсбЯжигАЯьЯчДхКЂзгЕФНЬг§ЮЪЬт,ЮЊДЫ,ФГЪаНёФъвЊЮЊФГЫљЯчДхжабЇеаЦИДЂБИЮДРДШ§ФъЕФНЬЪІ,ЯждкУПеаЦИвЛУћНЬЪІашвЊ2ЭђдЊ,ШєШ§ФъКѓНЬЪІбЯжиЖЬШБЪБдйеаЦИ,гЩгкИїжжвђЫи,дђУПеаЦИвЛУћНЬЪІашвЊ5ЭђдЊ,вбжЊЯждкИУЯчДхжабЇЮоЖргрНЬЪІ,ЮЊОіВпгІеаЦИЖрЩйЯчДхНЬЪІЫбМЏВЂећРэСЫИУЪа100ЫљЯчДхжабЇдкЙ§ШЅШ§ФъФкЕФНЬЪІСїЪЇЪ§,ЕУЕНШчЯТЕФжљзДЭМЃКМЧxБэЪОвЛЫљЯчДхжабЇдкЙ§ШЅШ§ФъФкСїЪЇЕФНЬЪІЪ§,yБэЪОвЛЫљЯчДхжабЇЮДРДЫФФъФкдкеаЦИНЬЪІЩЯЫљашЕФЗбгУ(ЕЅЮЛЃКЭђдЊ)ЃЌnБэЪОНёФъЮЊИУЯчДхжабЇеаЦИЕФНЬЪІЪ§ЃЌЮЊБЃеЯЯчДхКЂзгНЬг§ВЛЪмгАЯьЃЌШєЮДРДШ§ФъФкНЬЪІгаЖЬШБЃЌдђЕкЫФФъТэЩЯеаЦИ.

(1)Шєn=19ЃЌЧѓyгыxЕФКЏЪ§НтЮіЪНЃЛ
(2)ШєвЊЧѓЁАСїЪЇЕФНЬЪІЪ§ВЛДѓгкnЁБЕФЦЕТЪВЛаЁгк0.5ЃЌЧѓnЕФзюаЁжЕЃЛ
(3)МйЩшНёФъИУЪаЮЊет100ЫљЯчДхжабЇЕФУПвЛЫљЖМеаЦИСЫ19ИіНЬЪІЛђ20ИіНЬЪІЃЌЗжБ№МЦЫуИУЪаЮДРДЫФФъФкЮЊет100ЫљЯчДхжабЇеаЦИНЬЪІЫљашЗбгУЕФЦНОљЪ§ЃЌвдДЫзїЮЊОіВпвРОнЃЌНёФъИУЯчДхжабЇгІеаЦИ19УћЛЙЪЧ20УћНЬЪІ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЯђСП ![]() =ЃЈ2cosxЃЌtЃЉЃЈtЁЪRЃЉЃЌ
=ЃЈ2cosxЃЌtЃЉЃЈtЁЪRЃЉЃЌ ![]() =ЃЈsinxЉcosxЃЌ1ЃЉЃЌКЏЪ§y=fЃЈxЃЉ=
=ЃЈsinxЉcosxЃЌ1ЃЉЃЌКЏЪ§y=fЃЈxЃЉ= ![]()
![]() ЃЌНЋy=fЃЈxЃЉЕФЭМЯѓЯђзѓЦНвЦ
ЃЌНЋy=fЃЈxЃЉЕФЭМЯѓЯђзѓЦНвЦ ![]() ИіЕЅЮЛГЄЖШКѓЕУЕНy=gЃЈxЃЉЕФЭМЯѓЧвy=gЃЈxЃЉдкЧјМф[0ЃЌ
ИіЕЅЮЛГЄЖШКѓЕУЕНy=gЃЈxЃЉЕФЭМЯѓЧвy=gЃЈxЃЉдкЧјМф[0ЃЌ ![]() ]ФкЕФзюДѓжЕЮЊ
]ФкЕФзюДѓжЕЮЊ ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓtЕФжЕМАy=fЃЈxЃЉЕФзюаЁе§жмЦкЃЛ
ЃЈ2ЃЉЩшЁїABCЕФФкНЧAЃЌBЃЌCЕФЖдБпЗжБ№ЮЊaЃЌbЃЌcЃЌШє ![]() gЃЈ
gЃЈ ![]() Љ
Љ ![]() ЃЉ=Љ1ЃЌa=2ЃЌЧѓBCБпЩЯЕФИпЕФзюДѓжЕЃЎ
ЃЉ=Љ1ЃЌa=2ЃЌЧѓBCБпЩЯЕФИпЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈЂёЃЉЧѓ![]() ЕФЕЅЕїЧјМфЃЛ
ЕФЕЅЕїЧјМфЃЛ
ЃЈЂђЃЉЧѓ![]() дкЧјМф
дкЧјМф![]() ЩЯЕФзюаЁжЕ.
ЩЯЕФзюаЁжЕ.
ЁОД№АИЁПЃЈЂёЃЉ![]() ;ЃЈЂђЃЉ
;ЃЈЂђЃЉ![]() .
.
ЁОНтЮіЁПЃЈЂёЃЉ![]() .
.
Сю![]() ЃЌЕУ
ЃЌЕУ![]() .
.

![]() гы
гы![]() ЕФЧщПіШчЩЯЃК
ЕФЧщПіШчЩЯЃК
ЫљвдЃЌ![]() ЕФЕЅЕїЕнМѕЧјМфЪЧ
ЕФЕЅЕїЕнМѕЧјМфЪЧ![]() ЃЌЕЅЕїЕндіЧјМфЪЧ
ЃЌЕЅЕїЕндіЧјМфЪЧ![]() .
.
ЃЈЂђЃЉЕБ![]() ЃЌМД
ЃЌМД![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() дк
дк![]() ЩЯЕЅЕїЕндіЃЌ
ЩЯЕЅЕїЕндіЃЌ
Ыљвд![]() дкЧјМф
дкЧјМф![]() ЩЯЕФзюаЁжЕЮЊ
ЩЯЕФзюаЁжЕЮЊ![]() .
.
ЕБ![]() ЃЌМД
ЃЌМД![]() ЪБЃЌ
ЪБЃЌ
гЩЃЈЂёЃЉжЊ![]() дк
дк![]() ЩЯЕЅЕїЕнМѕЃЌдк
ЩЯЕЅЕїЕнМѕЃЌдк![]() ЩЯЕЅЕїЕндіЃЌ
ЩЯЕЅЕїЕндіЃЌ
Ыљвд![]() дкЧјМф
дкЧјМф![]() ЩЯЕФзюаЁжЕЮЊ
ЩЯЕФзюаЁжЕЮЊ![]() .
.
ЕБ![]() ЃЌМД
ЃЌМД![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() дк
дк![]() ЩЯЕЅЕїЕнМѕЃЌ
ЩЯЕЅЕїЕнМѕЃЌ
Ыљвд![]() дкЧјМф
дкЧјМф![]() ЩЯЕФзюаЁжЕЮЊ
ЩЯЕФзюаЁжЕЮЊ![]() .
.
злЩЯЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФзюаЁжЕЮЊ
ЕФзюаЁжЕЮЊ![]() ЃЛ
ЃЛ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФзюаЁжЕЮЊ
ЕФзюаЁжЕЮЊ![]() ЃЛ
ЃЛ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФзюаЁжЕЮЊ
ЕФзюаЁжЕЮЊ![]() .
.
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
19
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЕФЖЅЕудкдЕу,НЙЕудкзјБъжсЩЯЃЌЕу
ЕФЖЅЕудкдЕу,НЙЕудкзјБъжсЩЯЃЌЕу![]() ЮЊХзЮяЯп
ЮЊХзЮяЯп![]() ЩЯвЛЕу.
ЩЯвЛЕу.
ЃЈ1ЃЉЧѓ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉШєЕу![]() дк
дк![]() ЩЯЃЌЙ§
ЩЯЃЌЙ§![]() зї
зї![]() ЕФСНЯв
ЕФСНЯв![]() гы
гы![]() ЃЌШє
ЃЌШє![]() ЃЌЧѓжЄ: жБЯп
ЃЌЧѓжЄ: жБЯп![]() Й§ЖЈЕу.
Й§ЖЈЕу.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіжБНЧШ§НЧаЮЕФШ§ИіЖЅЕуЗжБ№дкЕзУцРтГЄЮЊ2ЕФе§Ш§РтжљЕФВрРтЩЯЃЌдђИУжБНЧШ§НЧаЮаББпЕФзюаЁжЕЮЊ__________ЃЎ
ЁОД№АИЁП![]()
ЁОНтЮіЁП ШчЭМЃЌВЛЗСЩш
ШчЭМЃЌВЛЗСЩш![]() дк
дк![]() ДІЃЌ
ДІЃЌ ![]() ЃЌ
ЃЌ
дђга![]() гЩ
гЩ![]()
![]() ИУжБНЧШ§НЧаЮаББп
ИУжБНЧШ§НЧаЮаББп![]()
ЙЪД№АИЮЊ![]() .
.
ЁОЬтаЭЁПЬюПеЬт
ЁОНсЪјЁП
16
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉЃН![]() ЃЌgЃЈxЃЉЃН
ЃЌgЃЈxЃЉЃН![]() ЃЌШєКЏЪ§yЃНfЃЈgЃЈxЃЉЃЉЃЋaгаШ§ИіВЛЭЌЕФСуЕуx1ЃЌx2ЃЌx3ЃЈЦфжаx1ЃМx2ЃМx3ЃЉЃЌдђ2gЃЈx1ЃЉЃЋgЃЈx2ЃЉЃЋgЃЈx3ЃЉЕФШЁжЕЗЖЮЇЮЊ______ЃЎ
ЃЌШєКЏЪ§yЃНfЃЈgЃЈxЃЉЃЉЃЋaгаШ§ИіВЛЭЌЕФСуЕуx1ЃЌx2ЃЌx3ЃЈЦфжаx1ЃМx2ЃМx3ЃЉЃЌдђ2gЃЈx1ЃЉЃЋgЃЈx2ЃЉЃЋgЃЈx3ЃЉЕФШЁжЕЗЖЮЇЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкШчЭМЫљЪОЕФШ§РтзЖABCЉA1B1C1жаЃЌAA1ЁЭЕзУцABCЃЌDЃЌEЗжБ№ЪЧBCЃЌA1B1ЕФжаЕуЃЎ 
ЃЈ1ЃЉЧѓжЄЃКDEЁЮЦНУцACC1A1ЃЛ
ЃЈ2ЃЉШєABЁЭBCЃЌAB=BCЃЌЁЯACB1=60ЁуЃЌЧѓжБЯпBCгыЦНУцAB1CЫљГЩНЧЕФе§ЧажЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊfЃЈxЃЉ=sinxЉcosxЃЌxЁЪ[0ЃЌ+ЁоЃЉЃЎ
ЃЈ1ЃЉжЄУїЃК ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉжЄУїЃКЕБaЁн1ЪБЃЌfЃЈxЃЉЁмeaxЉ2ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ,ЦфЭМЯёгыжБЯп
ЃЉ,ЦфЭМЯёгыжБЯп![]() ЯрСкСНИіНЛЕуЕФОрРыЮЊ
ЯрСкСНИіНЛЕуЕФОрРыЮЊ![]() ,Шє
,Шє![]() ЖдгкШЮвтЕФ
ЖдгкШЮвтЕФ![]() КуГЩСЂ, дђ
КуГЩСЂ, дђ![]() ЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
ЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕжаЃЌвбжЊдВCЕФдВаФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌАыОЖЮЊ ![]() ЃЌвдзјБъдЕуЮЊМЋЕуЃЌxжсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЎЃЌжБЯпlЕФВЮЪ§ЗНГЬЮЊЃК
ЃЌвдзјБъдЕуЮЊМЋЕуЃЌxжсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЎЃЌжБЯпlЕФВЮЪ§ЗНГЬЮЊЃК ![]() ЃЈtЮЊВЮЪ§ЃЉЃЎ
ЃЈtЮЊВЮЪ§ЃЉЃЎ
ЃЈ1ЃЉЧѓдВCКЭжБЯпlЕФМЋзјБъЗНГЬЃЛ
ЃЈ2ЃЉЕуPЕФМЋзјБъЮЊЃЈ1ЃЌ ![]() ЃЉЃЌжБЯпlгыдВCЯрНЛгкAЃЌBЃЌЧѓ|PA|+|PB|ЕФжЕЃЎ
ЃЉЃЌжБЯпlгыдВCЯрНЛгкAЃЌBЃЌЧѓ|PA|+|PB|ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com