
【题目】已知点E在椭圆![]() 上,以E为圆心的圆与x轴相切于椭圆C的右焦点
上,以E为圆心的圆与x轴相切于椭圆C的右焦点![]() ,与y轴相交于A,B两点,且
,与y轴相交于A,B两点,且![]() 是边长为2的正三角形.
是边长为2的正三角形.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知圆![]() ,设圆O上任意一点P处的切线交椭圆C于M、N两点,试判断以
,设圆O上任意一点P处的切线交椭圆C于M、N两点,试判断以![]() 为直径的圆是否过定点?若过定点,求出该定点坐标,并直接写出
为直径的圆是否过定点?若过定点,求出该定点坐标,并直接写出![]() 的值;若不过定点,请说明理由.
的值;若不过定点,请说明理由.
【答案】(Ⅰ)![]() (Ⅱ)以
(Ⅱ)以![]() 为直径的圆过原点,坐标为
为直径的圆过原点,坐标为![]() ,且
,且![]() 为定值
为定值![]()
【解析】
(Ⅰ)根据圆的切线性质可以知道![]() ,这样可以求出点E的坐标,利用等边三角形的性质,可以求出
,这样可以求出点E的坐标,利用等边三角形的性质,可以求出![]() 、
、![]() 的值,再根据
的值,再根据![]() ,最后求出
,最后求出![]() 的值,也就求出椭圆C的方程;
的值,也就求出椭圆C的方程;
(Ⅱ)当过点P且与圆O相切的切线的斜率不存在时,设出直线方程,求出M、N两点的坐标,判断![]() 是否成立,可以判断以
是否成立,可以判断以![]() 为直径的圆是否过定点,也就能求出
为直径的圆是否过定点,也就能求出![]() 的值;
的值;
当过点P且与圆O相切的切线的斜率存在时,设出直线的截距式方程![]() ,设出M、N两点的坐标,根据直线和圆相切,利用圆心到直线的距离等于半径,可得到一个等式,
,设出M、N两点的坐标,根据直线和圆相切,利用圆心到直线的距离等于半径,可得到一个等式,
联立直线方程![]() 和椭圆方程
和椭圆方程![]() ,消去
,消去![]() ,得到一个关于
,得到一个关于![]() 的一元二次方程,利用根与系数关系,计算
的一元二次方程,利用根与系数关系,计算![]() 的值,最后可以求出
的值,最后可以求出![]() 的值.
的值.
解:(Ⅰ)由题意可得![]() 轴,则
轴,则![]() ,
,
因为![]() 是边长为2的正三角形,
是边长为2的正三角形,
所以![]()
![]() ,且
,且![]() ,
,
解得![]() ,
,![]() ,
,
所以椭圆方程为![]() .
.
(Ⅱ)当过点P且与圆O相切的切线的斜率不存在时,
可设切线方程为![]() ,可得
,可得![]() ,
,![]() ,
,
则![]() ,所以
,所以![]() ,
,
此时以![]() 为直径的圆过原点,
为直径的圆过原点,
![]() 为定值;
为定值;
当过点P且与圆O相切的切线的斜率存在时,可设切线方程为![]() ,
,![]() ,
,![]() ,
,
由直线和圆相切可得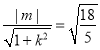 ,即
,即![]() ,
,
联立直线方程![]() 和椭圆方程
和椭圆方程![]() ,
,
可得![]() ,
,
即有![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
![]() ,
,
可得![]() ,
,
此时![]() .
.
综上可得以![]() 为直径的圆过原点,且
为直径的圆过原点,且![]() 为定值
为定值![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面ABCD,
平面ABCD,![]() 是等边三角形,四边形ABCD是矩形,
是等边三角形,四边形ABCD是矩形,![]() ,F为棱PA上一点,且
,F为棱PA上一点,且![]() ,M为AD的中点,四棱锥
,M为AD的中点,四棱锥![]() 的体积为
的体积为![]() .
.
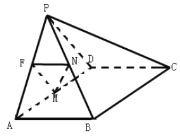
(1)若![]() ,N是PB的中点,求证:平面
,N是PB的中点,求证:平面![]() 平面PCD;
平面PCD;
(2)在(Ⅰ)的条件,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 为两条不同的直线,
为两条不同的直线, ![]() ,
, ![]() 为两个不同的平面,对于下列四个命题:
为两个不同的平面,对于下列四个命题:
①![]() ,
, ![]() ,
, ![]() ,
, ![]() ②
②![]() ,
, ![]()
③![]() ,
, ![]() ,
, ![]() ④
④![]() ,
, ![]()
其中正确命题的个数有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】禽流感一直在威胁我们的生活,某疾病控制中心为了研究禽流感病毒繁殖个数![]() (个)随时间
(个)随时间![]() (天)变化的规律,收集数据如下:
(天)变化的规律,收集数据如下:
天数 | 1 | 2 | 3 | 4 | 5 | 6 |
繁殖个数 | 6 | 12 | 25 | 49 | 95 | 190 |
作出散点图可看出样本点分布在一条指数型函数![]() 的周围.
的周围.
保留小数点后两位数的参考数据:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]()
(1)求出![]() 关于
关于![]() 的回归方程(保留小数点后两位数字);
的回归方程(保留小数点后两位数字);
(2)已知![]() ,估算第四天的残差.
,估算第四天的残差.
参考公式: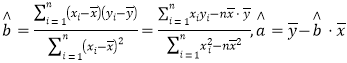
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】众所周知的“太极图”,其形状如对称的阴阳两鱼互抱在一起,因而也被称为“阴阳鱼太极图”.如图是放在平面直角坐标系中的“太极图”,整个图形是一个圆形,其中黑色阴影区域在y轴右侧部分的边界为一个半圆.给出以下命题:

①在太极图中随机取一点,此点取自黑色阴影部分的概率是![]() ;
;
②当![]() 时,直线
时,直线![]() 与黑色阴影部分有公共点;
与黑色阴影部分有公共点;
③当![]() 时,直线
时,直线![]() 与黑色阴影部分有两个公共点.
与黑色阴影部分有两个公共点.
其中所有正确结论的序号是()
A.①B.②C.③D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,如果存在常数p,使得对任意正整数n,总有
,如果存在常数p,使得对任意正整数n,总有![]() 成立,那么我们称数列
成立,那么我们称数列![]() 为“p-摆动数列”.
为“p-摆动数列”.
(Ⅰ)设![]() ,
,![]() ,
,![]() ,判断
,判断![]() 、
、![]() 是否为“p-摆动数列”,并说明理由;
是否为“p-摆动数列”,并说明理由;
(Ⅱ)已知“p-摆动数列”![]() 满足
满足![]() ,
,![]() ,求常数p的值;
,求常数p的值;
(Ⅲ)设![]() ,且数列
,且数列![]() 的前n项和为
的前n项和为![]() ,求证:数列
,求证:数列![]() 是“p-摆动数列”,并求出常数p的取值范围.
是“p-摆动数列”,并求出常数p的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
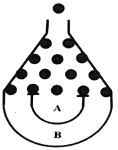
【题目】某超市国庆大酬宾,购物满100元可参加一次游戏抽奖活动,游戏抽奖规则如下:顾客将一个半径适当的小球放入如图所示的容器正上方的入口处,小球自由落下过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,落入A袋得奖金4元,落入B袋得奖金8元,已知小球每次遇到黑色障碍物时,向左向右下落的概率都为![]() .已知李女士当天在该超市购物消费128元,按照活动要求,李女士的活动奖金期望值为_____元.
.已知李女士当天在该超市购物消费128元,按照活动要求,李女士的活动奖金期望值为_____元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com