
【题目】某学校高三年级有![]() 、
、![]() 两个自习教室,甲、乙、丙
两个自习教室,甲、乙、丙![]() 名学生各自随机选择其中一个教室自习,则甲、乙两人不在同一教室上自习的概率为________.
名学生各自随机选择其中一个教室自习,则甲、乙两人不在同一教室上自习的概率为________.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点为
,右焦点为![]() ,左顶点为A,右顶点B在直线
,左顶点为A,右顶点B在直线![]() 上.
上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点P是椭圆C上异于A,B的点,直线![]() 交直线
交直线![]() 于点
于点![]() ,当点
,当点![]() 运动时,判断以
运动时,判断以![]() 为直径的圆与直线PF的位置关系,并加以证明.
为直径的圆与直线PF的位置关系,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用细钢管焊接而成的花坛围栏构件如图所示,它的外框是一个等腰梯形PQRS,内部是一段抛物线和一根横梁,抛物线的顶点与梯形上底中点是焊接点O,梯形的腰紧靠在抛物线上,两条腰的中点是梯形的腰、抛物线以及横梁的焊接点A,B,抛物线与梯形下底的两个焊接点为C,D,已知梯形的高是40厘米,C,D两点间的距离为40厘米.
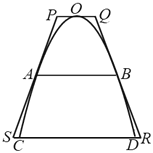
(1)求横梁AB的长度;
(2)求梯形外框的用料长度;
(注:细钢管的粗细等因素忽略不计,结果精确到1厘米)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线
为直线![]() 的倾斜角),以坐标原点
的倾斜角),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 时直线
时直线![]() 的普通方程;
的普通方程;
(2)直线![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的首项
的首项![]() ,对任意的
,对任意的![]() ,都有
,都有![]() ,数列
,数列![]() 是公比不为
是公比不为![]() 的等比数列.
的等比数列.
(1)求实数![]() 的值;
的值;
(2)设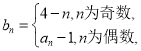 数列
数列![]() 的前
的前![]() 项和为
项和为![]() ,求所有正整数
,求所有正整数![]() 的值,使得
的值,使得![]() 恰好为数列
恰好为数列![]() 中的项.
中的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在△![]() 中,
中, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,
的中点, ![]() 为
为![]() 的中点,
的中点, ![]() ,
, ![]() .将△
.将△![]() 沿
沿![]() 折起到△
折起到△![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,
, ![]() 为
为![]() 的中点,如图2.
的中点,如图2.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级有男生![]() 人,编号为
人,编号为![]() ,
,![]() ,…,
,…,![]() ;女生
;女生![]() 人,编号为
人,编号为![]() ,
,![]() ,…,
,…,![]() .为了解学生的学习状态,按编号采用系统抽样的方法从这
.为了解学生的学习状态,按编号采用系统抽样的方法从这![]() 名学生中抽取
名学生中抽取![]() 人进行问卷调查,第一组抽到的号码为
人进行问卷调查,第一组抽到的号码为![]() ,现从这
,现从这![]() 名学生中随机抽取
名学生中随机抽取![]() 人进行座谈,则这
人进行座谈,则这![]() 人中既有男生又有女生的概率是( )
人中既有男生又有女生的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com