
【题目】如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是( ) 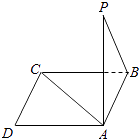
A.90°
B.60°
C.45°
D.30°
【答案】B
【解析】解:将其还原成正方体ABCD﹣PQRS,连接SC,AS,则PB∥SC,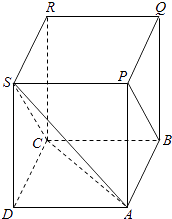
∴∠ACS(或其补角)是PB与AC所成的角
∵△ACS为正三角形,
∴∠ACS=60°
∴PB与AC所成的角是60°
故选B.
【考点精析】掌握异面直线及其所成的角和直线与平面垂直的判定是解答本题的根本,需要知道异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 分别为等差数列和等比数列,
分别为等差数列和等比数列, ![]() ,
, ![]() 的前
的前![]() 项和为
项和为![]() .函数
.函数![]() 的导函数是
的导函数是![]() ,有
,有![]() ,且
,且![]() 是函数
是函数![]() 的零点.
的零点.
(1)求![]() 的值;
的值;
(2)若数列![]() 公差为
公差为![]() ,且点
,且点![]() ,当
,当![]() 时所有点都在指数函数
时所有点都在指数函数![]() 的图象上.
的图象上.
请你求出![]() 解析式,并证明:
解析式,并证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人有楼房一幢,室内面积共计180m2 , 拟分割成两类房间作为旅游客房,大房间每间面积为18m2 , 可住游客5名,每名游客每天住宿费40元;小房间每间面积为15m2 , 可以住游客3名,每名游客每天住宿费50元;装修大房间每间需要1000元,装修小房间每间需要600元.如果他只能筹款8000元用于装修,且假定游客能住满客房,他应隔出大房间和小房间各多少间,才能获得最大收益? 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={f(x)|f2(x)﹣f2(y)=f(x+y)f(x﹣y),x,y∈R},有下列命题
①若f(x)= ![]() ,则f(x)∈M;
,则f(x)∈M;
②若f(x)=2x,则f(x)∈M;
③f(x)∈M,则y=f(x)的图象关于原点对称;
④f(x)∈M,则对于任意实数x1 , x2(x1≠x2),总有 ![]() <0成立;
<0成立;
其中所有正确命题的序号是 . (写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 和
和![]() 的通项公式分别为
的通项公式分别为![]() ,将集合
,将集合![]()
![]() 中的元素从小到大依次排列,构成数列
中的元素从小到大依次排列,构成数列![]() ;将集合
;将集合![]()
![]() 中的元素从小到大依次排列,构成数列
中的元素从小到大依次排列,构成数列![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)求数列![]() 的通项公式
的通项公式![]() ;
;
(3)设数列![]() 的前
的前![]() 项和为
项和为![]() ,求数列
,求数列![]() 的通项公式
的通项公式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C的中心为原点O,F(﹣2 ![]() ,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=4,则椭圆C的方程为( )
,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=4,则椭圆C的方程为( ) 
A.![]() =1
=1
B.![]() =1
=1
C.![]() =1
=1
D.![]() =1
=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com