【题目】已知椭圆
： 
，椭圆
以
的长轴为短轴，且与
有相同的离心率.
（1）求椭圆
的方程；
（2）设
为坐标原点，点
分别在椭圆
和
上， 
，求直线
的方程.
【答案】（1）
（2）
或
【解析】试题分析：（1）求出椭圆
： 
的长轴长，离心率，根据椭圆C2以C1的长轴为短轴，且与C1有相同的离心率，即可确定椭圆C2的方程；（2）设A，B的坐标分别为
，根据
，可设AB的方程为y=kx，分别与椭圆C1和C2联立，求出A，B的横坐标，利用
，即可求得直线AB的方程．
试题解析：（1）由已知可设椭圆
的方程为
（
），
其离心率为
，故
，则
，
故椭圆
的方程为
.
（2）解法一： 
两点的坐标分别为
，由
及（1）知， 
三点共线且点
不在
轴上，因此可设直线
的方程为
.
将
代入
中，得
，所以
，
将
代入
中，得
，所以
，
又由
，得
，即
，
解得
，故直线
的方程为
或
.
解法二： 
两点的坐标分别为
，由
及（1）知， 
三点共线且点
不在
轴上，因此可设直线
的方程为
.
将
代入
中，得
，所以
，
又由
，得
， 
，
将
代入
中，得
，即
，
解得
，故直线
的方程为
或
.
芝麻开花课程新体验系列答案科目：高中数学 来源： 题型：
【题目】某校高二（1）班学生为了筹措经费给班上购买课外读物，班委会成立了一个社会实践小组，决定利用暑假八月份（30天计算）轮流换班去销售一种时令水果.在这30天内每斤水果的收入
（元）与时间
（天）的部分数据如下表所示，已知日销售
（斤）与时间
（天）满足一次函数关系.
（1）根据提供的图象和表格，下厨每斤水果的收入
（元）与时间
（天）所满足的函数关系式及日销售量
（斤）与时间
（天）的一次函数关系；
（2）用
（元）表示销售水果的日收入，写出
与
的函数关系式，并求这30天中第几天日收入最大，最大值为多少元？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设a是实数，f（x）=a﹣ 
（x∈R）．
（1）证明不论a为何实数，f（x）均为增函数；
（2）若f（x）满足f（﹣x）+f（x）=0，解关于x的不等式f（x+1）+f（1﹣2x）＞0．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在测试中，客观题难题的计算公式为
，其中
为第
题的难度， 
为答对该题的人数， 
为参加测试的总人数.现对某校高三年级120名学生进行一次测试，共5道客观题.测试前根据对学生的了解，预估了每道题的难度，如下表所示：
测试后，从中随机抽取了10名学生，将他们编号后统计各题的作答情况，如下表所示（“√”表示答对，“×”表示答错）：
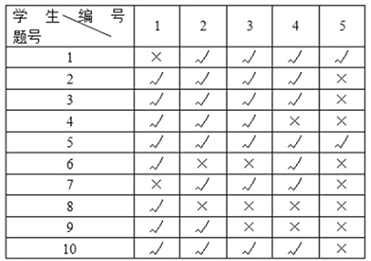
（1）根据题中数据，将抽样的10名学生每道题实测的答对人数及相应的实测难度填入下表，并估计这120名学生中第5题的实测答对人数；
（2）从编号为1到5的5人中随机抽取2人，求恰好有1人答对第5题的概率；
（3）定义统计量
，其中
为第
题的实测难度， 
为第
题的预估难度（
）.规定：若
，则称该次测试的难度预估合理，否则为不合理.判断本次测试的难度预估是否合理.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，点P在正方形ABCD所在平面外，PA⊥平面ABCD，PA=AB，则PB与AC所成的角是（ ）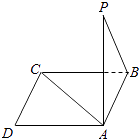 
A.90°
B.60°
C.45°
D.30°
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知曲线
，曲线
， 
是平面上一点，若存在过点
的直线与
都有公共点，则称
为“
型点”.
（1）证明： 
的左焦点是“
型点”；
（2）设直线
与
有公共点，求证： 
，进而证明原点不是“
型点”；
（3）求证： 
内的点都不是“
型点”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
