
【题目】如图,在长方体A1B1C1D1﹣ABCD中,AD=CD=4,AD1=5,M是线段B1D1的中点. 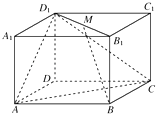
(1)求证:BM∥平面D1AC;
(2)求直线DD1与平面D1AC所成角的正弦值.
【答案】
(1)解:在长方体A1B1C1D1﹣ABCD中,
∵AD=4,AD1=5,∴DD1= ![]() =3,
=3,
以D为原点,DA,DA,DD1分别为xyz轴建立空间直角坐标系D﹣xyz,
根据题意得A(4,0,0),B(4,4,0),C(0,4,0),D(0,0,0),
B1(4,4,3),D1(0,0,3),线段B1D1的中点为M(2,2,3),线段AC的中点为N(2,2,0).
∴ ![]() =(﹣2,﹣2,3),
=(﹣2,﹣2,3), ![]() =(﹣2,﹣2,3).∴
=(﹣2,﹣2,3).∴ ![]() ∥
∥ ![]() ,∴BM∥ND1.
,∴BM∥ND1.
∵BM平面D1AC,ND1平面D1AC,∴BM∥平面D1AC
(2)解:∵ ![]() =(0,0,3),
=(0,0,3), ![]() =(﹣4,4,0),
=(﹣4,4,0), ![]() =(﹣4,0,3),
=(﹣4,0,3),
设平面D1AC的法向量为 ![]() =(x,y,z),
=(x,y,z),
根据已知得 ![]() =﹣4x+4y=0,且
=﹣4x+4y=0,且 ![]() =﹣4x+3z=0,
=﹣4x+3z=0,
取x=1,可得y=1,z= ![]() ,∴
,∴ ![]() =(1,1,
=(1,1, ![]() )是平面D1AC的一个法向量,
)是平面D1AC的一个法向量,
∴cos< ![]() ,
, ![]() >=
>= 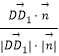 =
= ![]() ,
,
∴直线DD1与平面D1AC所成角的正弦值等于 ![]()
【解析】(1)以D为原点,DA,DA,DD1分别为xyz轴建立空间直角坐标系D﹣xyz,由坐标法可证 ![]() ∥
∥ ![]() ,进而可得BM∥ND1 . 由线面平行的判定定理可得;(2)设平面D1AC的法向量为
,进而可得BM∥ND1 . 由线面平行的判定定理可得;(2)设平面D1AC的法向量为 ![]() =(x,y,z),根据
=(x,y,z),根据 ![]() =﹣4x+4y=0,且
=﹣4x+4y=0,且 ![]() =﹣4x+3z=0,可求,进而可得cos<
=﹣4x+3z=0,可求,进而可得cos< ![]() ,
, ![]() >,即得所求.
>,即得所求.
【考点精析】掌握直线与平面平行的判定和空间角的异面直线所成的角是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则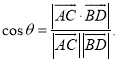 .
.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:
【题目】将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为x,第二次出现的点数为y.
(1)求事件“x+y≤3”的概率;
(2)求事件“|x﹣y|=2”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 顶点在原点,焦点在
顶点在原点,焦点在![]() 轴上,抛物线
轴上,抛物线![]() 上一点
上一点![]() 到焦点的距离为3,线段
到焦点的距离为3,线段![]() 的两端点
的两端点![]() ,
, ![]() 在抛物线
在抛物线![]() 上.
上.
(1)求抛物线![]() 的方程;
的方程;
(2)若![]() 轴上存在一点
轴上存在一点![]() ,使线段
,使线段![]() 经过点
经过点![]() 时,以
时,以![]() 为直径的圆经过原点,求
为直径的圆经过原点,求![]() 的值;
的值;
(3)在抛物线![]() 上存在点
上存在点![]() ,满足
,满足![]() ,若
,若![]() 是以角
是以角![]() 为直角的等腰直角三角形,求
为直角的等腰直角三角形,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对新研究的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x元 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销售y件 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程 ![]() ,其中
,其中 ![]() =﹣20.
=﹣20.
(2)预计在今后的销售中,销售与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价定为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos4x﹣2sinxcosx﹣sin4x.
(1)求f(x)的最小正周期及对称中心;
(2)当x∈[0, ![]() ]时,求f(x)的单调递减区间.
]时,求f(x)的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[x]表示不超过x的最大整数,例如:[π]=3. S1=[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]=3
]=3
S2=[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]=10
]=10
S3=[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+
]+ ![]() ]=21,
]=21,
…,
依此规律,那么S10=( )
A.210
B.230
C.220
D.240
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx(a,b为常数,且a≠0)满足条件:f(x﹣1)=f(3﹣x),且方程f(x)=2x有两等根.
(1)求f(x)的解析式.
(2)求f(x)在[0,t]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数),其图像是曲线
为常数),其图像是曲线![]() .
.
(1)设函数![]() 的导函数为
的导函数为![]() ,若存在三个实数
,若存在三个实数![]() ,使得
,使得![]() 与
与![]() 同时成立,求实数
同时成立,求实数![]() 的取值范围;
的取值范围;
(2)已知点![]() 为曲线
为曲线![]() 上的动点,在点
上的动点,在点![]() 处作曲线
处作曲线![]() 的切线
的切线![]() 与曲线
与曲线![]() 交于另一点
交于另一点![]() ,在点
,在点![]() 处作曲线
处作曲线![]() 的切线
的切线![]() ,设切线
,设切线![]() 的斜率分别为
的斜率分别为![]() ,问:是否存在常数
,问:是否存在常数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数已知函数f(x)=x3+ax2+bx+c在x=﹣ ![]() 和x=1处取得极值.
和x=1处取得极值.
(1)求a,b的值及其单调区间;
(2)若对x∈[﹣1,2]不等式f(x)≤c2恒成立,求c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com