
【题目】设函数f(x)= ![]() ,g(x)=lnx+
,g(x)=lnx+ ![]() (a>0).
(a>0).
(1)求函数f(x)的极值;
(2)若x1、x2∈(0,+∞),使得g(x1)≤f(x2)成立,求a的取值范围.
【答案】
(1)解:f′(x)= ![]() =
= ![]() ,
,
令f′(x)=0,解得x=0,2.
列表如下:
x | (﹣∞,0) | 0 | (0,2) | 2 | (2,+∞) |
f′(x) | ﹣ | 0 | + | 0 | ﹣ |
f(x) | 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
可知:当x=0时,函数f(x)取得极小值,f(0)=0.当x=2时,函数f(x)取得极大值,f(2)= ![]()
(2)解:x1、x2∈(0,+∞),使得g(x1)≤f(x2)成立,[g(x)]min≤[f(x)]max,x∈(0,+∞).
由(1)可得:[f(x)]max=f(2)= ![]() .
.
g′(x)= ![]() ﹣
﹣ ![]() =
= ![]() (x>0,a>0).
(x>0,a>0).
可知:当x=a时,函数g(x)取得极小值即最小值,
∴g(a)=lna+1≤ ![]() .
.
∴0<a≤ ![]() .
.
因此a的取值范围是 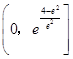
【解析】(1)f′(x)= ![]() ,令f′(x)=0,解得x=0,2.列表如下,即可得出极值.(2)x1、x2∈(0,+∞),使得g(x1)≤f(x2)成立[g(x)]min≤[f(x)]max,x∈(0,+∞).由(1)可得:[f(x)]max=f(2)=
,令f′(x)=0,解得x=0,2.列表如下,即可得出极值.(2)x1、x2∈(0,+∞),使得g(x1)≤f(x2)成立[g(x)]min≤[f(x)]max,x∈(0,+∞).由(1)可得:[f(x)]max=f(2)= ![]() .再利用导数研究函数g(x)的单调性即可得出极小值即最小值.
.再利用导数研究函数g(x)的单调性即可得出极小值即最小值.
【考点精析】通过灵活运用函数的极值与导数和函数的最大(小)值与导数,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值;求函数
是极小值;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.
比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知![]() 和定点
和定点![]() ,由
,由![]() 外一点
外一点![]() 向
向![]() 引切线
引切线![]() ,切点为
,切点为![]() ,且满足
,且满足![]() .(1)求实数
.(1)求实数![]() 间满足的等量关系;
间满足的等量关系;
(2)求线段![]() 长的最小值;
长的最小值;
(3)若以![]() 为圆心所作的
为圆心所作的![]() 与
与![]() 有公共点,试求半径取最小值时的
有公共点,试求半径取最小值时的![]() 方程.
方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+![]() (a>1),
(a>1),
(1)判断函数f(x)在(-1,+∞)上的单调性,并证明你的判断;
(2)若a=3,求方程f(x)=0的正根(精确到0.1).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在半径为![]() 的半圆形(
的半圆形(![]() 为圆心)铝皮上截取一块矩形材料
为圆心)铝皮上截取一块矩形材料![]() ,其中
,其中![]() 在直径上,点
在直径上,点![]() 在圆周上.
在圆周上.
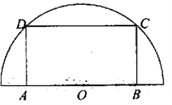
(1)设![]() ,将矩形
,将矩形![]() 的面积
的面积![]() 表示成
表示成![]() 的函数,并写出其定义域;
的函数,并写出其定义域;
(2)怎样截取,才能使矩形材料![]() 的面积最大?并求出最大面积.
的面积最大?并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+2x﹣2﹣a(a≤0),
(1)若a=﹣1,求函数的零点;
(2)若函数在区间(0,1]上恰有一个零点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数h(x)=ax3+bx2+cx+d(a≠0)图象的对称中心为M(x0 , h(x0)),记函数h(x)的导函数为g(x),则有g′(x0)=0,设函数f(x)=x3﹣3x2+2,则f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )+f(
)+f( ![]() )= .
)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个服装店经营某种服装,在某周内获纯利y(元)与该周每天销售这些服装件数x之间有如下一组数据:
x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
已知![]() =280,
=280, ![]() yi=3 487,
yi=3 487,
(1)求![]() ;
;
(2)求纯利y与每天销售件数x之间的回归直线方程;
(3)每天多销售1件,纯利y增加多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com