
【题目】已知![]() 和定点
和定点![]() ,由
,由![]() 外一点
外一点![]() 向
向![]() 引切线
引切线![]() ,切点为
,切点为![]() ,且满足
,且满足![]() .(1)求实数
.(1)求实数![]() 间满足的等量关系;
间满足的等量关系;
(2)求线段![]() 长的最小值;
长的最小值;
(3)若以![]() 为圆心所作的
为圆心所作的![]() 与
与![]() 有公共点,试求半径取最小值时的
有公共点,试求半径取最小值时的![]() 方程.
方程.
【答案】(1)![]() .(2)
.(2)![]() .(3)
.(3)![]() .
.
【解析】试题分析:(1)连![]() ,由勾股定理可得
,由勾股定理可得![]() ,化简可得实数
,化简可得实数![]() 间满足的等量关系;(2)由于
间满足的等量关系;(2)由于![]() ,根据
,根据![]() 间的等量关系及二次函数的性质即可求出线段
间的等量关系及二次函数的性质即可求出线段![]() 长的最小值;(3)解法一:设
长的最小值;(3)解法一:设![]() 的半径为
的半径为![]() ,根据题设条件可得
,根据题设条件可得![]() ,利用二次函数的性质求得
,利用二次函数的性质求得![]() 的最小值,此时,求得
的最小值,此时,求得![]() ,
, ![]() 取得最小值,从而得到圆的方程;解法二:根据
取得最小值,从而得到圆的方程;解法二:根据![]() 的轨迹设出直线
的轨迹设出直线![]() ,由
,由![]() 与
与![]() 有公共点,欲求半径最小,即为
有公共点,欲求半径最小,即为![]() 与
与![]() 外切时半径最小,然后可求出半径最小值及垂直直线
外切时半径最小,然后可求出半径最小值及垂直直线![]() 的方程,即可求出此时圆心
的方程,即可求出此时圆心![]() 的坐标,故而求出
的坐标,故而求出![]() 方程.
方程.
试题解析:(1)连![]()
∵![]() 为切点,
为切点, ![]() ,由勾股定理有
,由勾股定理有![]()
又由已知![]() ,故
,故![]() .即:
.即: ![]() .
.
化简得实数![]() 间满足的等量关系为:
间满足的等量关系为: ![]() .
.
(2)由![]() ,得
,得![]() .
.
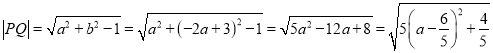 .
.
故当![]() 时,
时, ![]() ,即线段
,即线段![]() 长的最小值为
长的最小值为![]() .
.
(3)解法一:设![]() 的半径为
的半径为![]()
∵![]() 与
与![]() 有公共点,
有公共点, ![]() 的半径为1,
的半径为1,
∴![]() .即
.即![]() 且
且![]() .
.
而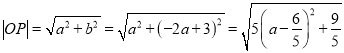 ,
,
故当![]() 时,
时, ![]() .此时,
.此时, ![]() ,
, ![]() .
.
得半径取最小值时![]() 的方程为
的方程为![]() .
.
解法二:由题意可得![]() 的轨迹方程是
的轨迹方程是![]() ,设为直线
,设为直线![]()
![]() 与
与![]() 有公共点,
有公共点, ![]() 半径最小时为与
半径最小时为与![]() 外切(取小者)的情形,而这些半径的最小值为圆心
外切(取小者)的情形,而这些半径的最小值为圆心![]() 到直线
到直线![]() 的距离减去1,圆心
的距离减去1,圆心![]() 为过原点与
为过原点与![]() 垂直的直线
垂直的直线![]() 与
与![]() 的交点
的交点![]() .
.
![]() .
.
又![]() ,
,
解方程组![]() ,得
,得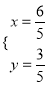 ,即
,即![]() .
.
∴所求圆方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资![]() 类产品的收益与投资额成正比,投资
类产品的收益与投资额成正比,投资![]() 类产品的收益与投资额的算术平方根成正比.已知投资1万元时
类产品的收益与投资额的算术平方根成正比.已知投资1万元时![]() 两类产品的收益分别为0.125万元和0.5万元.
两类产品的收益分别为0.125万元和0.5万元.
(1)分别写出![]() 两类产品的收益与投资额的函数关系;
两类产品的收益与投资额的函数关系;
(2)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设z1 , z2是复数,则下列命题中的假命题是( )
A.若|z1﹣z2|=0,则 ![]() =
= ![]()
B.若z1= ![]() ,则
,则 ![]() =z2
=z2
C.若|z1|=|z2|,则z1 ![]() =z2
=z2 ![]()
D.若|z1|=|z2|,则z12=z22
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2ax+5(a>1).
(1)若f(x)的定义域和值域均是[1,a],求实数a的值;
(2)若f(x)在区间(﹣∞,2]上是减函数,且对任意的x∈[1,a+1],总有f(x)≤0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了缓解交通压力,某省在两个城市之间特修一条专用铁路,用一列火车作为公共交通车.已知每日来回趟数y是每次拖挂车厢节数x的一次函数,如果该列火车每次拖4节车厢,每日能来回16趟;如果每次拖6节车厢,则每日能来回10趟,火车每日每次拖挂车厢的节数是相同的,每节车厢满载时能载客110人.
(1)求出y关于x的函数;
(2)该火车满载时每次拖挂多少节车厢才能使每日营运人数最多?并求出每天最多的营运人数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列结论:
,给出下列结论:
(1)若对任意![]() ,且
,且![]() ,都有
,都有![]() ,则
,则![]() 为R上的减函数;
为R上的减函数;
(2)若![]() 为R上的偶函数,且在
为R上的偶函数,且在![]() 内是减函数,
内是减函数, ![]() (-2)=0,则
(-2)=0,则![]() >0解集为(-2,2);
>0解集为(-2,2);
(3)若![]() 为R上的奇函数,则
为R上的奇函数,则![]() 也是R上的奇函数;
也是R上的奇函数;
(4)t为常数,若对任意的![]() ,都有
,都有![]() 则
则![]() 关于
关于![]() 对称。
对称。
其中所有正确的结论序号为_________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ,g(x)=lnx+
,g(x)=lnx+ ![]() (a>0).
(a>0).
(1)求函数f(x)的极值;
(2)若x1、x2∈(0,+∞),使得g(x1)≤f(x2)成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com