
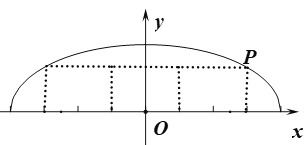
【题目】某高速公路隧道设计为单向三车道,每条车道宽4米,要求通行车辆限高5米,隧道全长1.5千米,隧道的断面轮廓线近似地看成半个椭圆形状(如图所示).

(1)若最大拱高![]() 为6米,则隧道设计的拱宽
为6米,则隧道设计的拱宽![]() 至少是多少米?(结果取整数)
至少是多少米?(结果取整数)
(2)如何设计拱高![]() 和拱宽
和拱宽![]() ,才能使半个椭圆形隧道的土方工程量最小?(结果取整数)
,才能使半个椭圆形隧道的土方工程量最小?(结果取整数)
参考数据:![]() ,椭圆的面积公式为
,椭圆的面积公式为![]() ,其中
,其中![]() ,
,![]() 分别为椭圆的长半轴和短半轴长.
分别为椭圆的长半轴和短半轴长.
【答案】(1)此隧道设计的拱宽![]() 至少是22米(2)当拱高为7米、拱宽为18米时,土方工程量最小
至少是22米(2)当拱高为7米、拱宽为18米时,土方工程量最小
【解析】
(1)建立直角坐标系,设椭圆方程为![]() ,根据对称性
,根据对称性![]() ,将点
,将点![]() 代入椭圆方程,即可求解;
代入椭圆方程,即可求解;
(2)由点![]() 在椭圆上或在椭圆内,得
在椭圆上或在椭圆内,得![]() ,利用基本不等式,即可求出椭圆的面积
,利用基本不等式,即可求出椭圆的面积![]() 的最小值,根据体积公式,即可求解.
的最小值,根据体积公式,即可求解.
(1)建立直角坐标系![]() 如图所示,
如图所示,
则点![]() 在椭圆
在椭圆![]() 上,
上,
将![]() 与点
与点![]() 代入椭圆方程,得
代入椭圆方程,得![]() ,
,
此时![]() ,
,
因此隧道设计的拱宽![]() 至少是22米.
至少是22米.
(2)由椭圆方程![]() ,得
,得![]() ,
,
因为![]() ,即
,即![]() ,
,![]() ,
,
由于隧道长度为1.5千米,故隧道的土方工程量![]() ,
,
当![]() 取得最小值时,有
取得最小值时,有![]() 且
且![]() ,得
,得![]() ,
,![]() ,
,
此时![]() ,
,![]() .
.
①若![]() ,此时
,此时![]() ,此时
,此时![]() ,
,
②若![]() ,此时
,此时![]() ,此时
,此时![]() ,
,
因为![]() ,故当拱高为7米、拱宽为18米时,土方工程量最小.
,故当拱高为7米、拱宽为18米时,土方工程量最小.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】某乐园按时段收费,收费标准为:每玩一次不超过![]() 小时收费10元,超过
小时收费10元,超过![]() 小时的部分每小时收费
小时的部分每小时收费![]() 元(不足
元(不足![]() 小时的部分按
小时的部分按![]() 小时计算).现有甲、乙二人参与但都不超过
小时计算).现有甲、乙二人参与但都不超过![]() 小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
(1) 用![]() 表示甲乙玩都不超过
表示甲乙玩都不超过![]() 小时的付费情况,求甲、乙二人付费之和为44元的概率;
小时的付费情况,求甲、乙二人付费之和为44元的概率;
(2)抽奖活动的规则是:顾客通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数![]() ,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.
,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据指令![]() (
(![]() ,
,![]() ),机器人在平面上能完成下列动作,先原地旋转弧度
),机器人在平面上能完成下列动作,先原地旋转弧度![]() (
(![]() 为正时,按逆时针方向旋转
为正时,按逆时针方向旋转![]() ,
,![]() 为负时,按顺时针方向旋转
为负时,按顺时针方向旋转![]() ),再朝其面对的方向沿直线行走距离r;
),再朝其面对的方向沿直线行走距离r;
(1)现机器人在平面直角坐标系的坐标原点,且面对x轴正方向,试给机器人下一个指令,使其移动到点![]() ;
;
(2)机器人在完成该指令后,发现在点![]() 处有一小球,正向坐标原点作匀速直线滚动,已知小球滚动的速度为机器人直线行走速度的2倍,若忽略机器人原地旋转所需的时间,问机器人最快可在何处截住小球?并给出机器人截住小球所需的指令?(结果用反三角函数表示)
处有一小球,正向坐标原点作匀速直线滚动,已知小球滚动的速度为机器人直线行走速度的2倍,若忽略机器人原地旋转所需的时间,问机器人最快可在何处截住小球?并给出机器人截住小球所需的指令?(结果用反三角函数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四面体A-BCD中,有两条棱的长为![]()
![]() ,其余棱的长度都为1;
,其余棱的长度都为1;
(1)若![]() ,且
,且![]() ,求二面角A-BC-D的余弦值;
,求二面角A-BC-D的余弦值;
(2)求a的取值范围,使得这样的四面体是存在的;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《郑州市城市生活垃圾分类管理办法》已经政府常务会议审议通过,自2019年12月1日起施行.垃圾分类是对垃圾收集处置传统方式的改革,是对垃圾进行有效处置的一种科学管理方法.所谓垃圾其实都是资源,当你放错了位置时它才是垃圾.某企业在市科研部门的支持下进行研究,把厨余垃圾加工处理为一种可销售的产品.已知该企业每周的加工处理量最少为75吨,最多为100吨.周加工处理成本y(元)与周加工处理量x(吨)之间的函数关系可近似地表示为![]() ,且每加工处理一吨厨余垃圾得到的产品售价为16元.
,且每加工处理一吨厨余垃圾得到的产品售价为16元.
(Ⅰ)该企业每周加工处理量为多少吨时,才能使每吨产品的平均加工处理成本最低?
(Ⅱ)该企业每周能否获利?如果获利,求出利润的最大值;如果不获利,则需要市政府至少补贴多少元才能使该企业不亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的渐近线方程为
的渐近线方程为![]() ,一个焦点为
,一个焦点为![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)过双曲线![]() 上的任意一点
上的任意一点![]() ,分别作这两条渐近线的平行线与这两条渐近线得到四边形
,分别作这两条渐近线的平行线与这两条渐近线得到四边形![]() ,证明四边形
,证明四边形![]() 的面积是一个定值;
的面积是一个定值;
(3)设直线![]() 与
与![]()
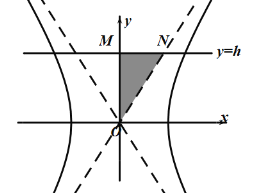
![]() 在第一象限内与渐近线
在第一象限内与渐近线![]() 所围成的三角形
所围成的三角形![]() 绕着
绕着![]() 轴旋转一周所得几何体的体积.
轴旋转一周所得几何体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 与
与![]() 轴相切于点
轴相切于点![]() ,与
,与![]() 轴正半轴相交于
轴正半轴相交于![]() 、
、![]() 两点,且
两点,且![]() ,如图1.
,如图1.
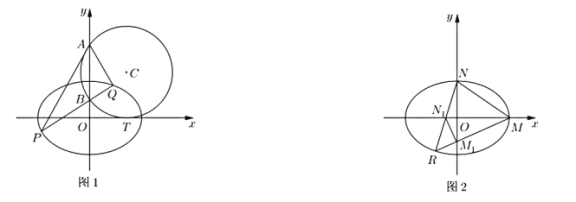
(1)求圆![]() 的方程;
的方程;
(2)如图1,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,求证:射线
两点,求证:射线![]() 平分
平分![]() ;
;
(3)如图2所示,点![]() 、
、![]() 是椭圆
是椭圆![]() 的两个顶点,且第三象限的动点
的两个顶点,且第三象限的动点![]() 在椭圆
在椭圆![]() 上,若直线
上,若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,试问:四边形
,试问:四边形![]() 的面积是否为定值?若是,请求出这个定值,若不是,请说明理由.
的面积是否为定值?若是,请求出这个定值,若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com