练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆的离心率为，上顶点为A，右顶点为B.点在椭圆C内，且直线与直线垂直.

    （1）求C的方程；

    （2）设过点P的直线交C于M，N两点，求证：以为直径的圆过点.

    【答案】（1）（2）见解析

    【解析】

    (1)根据椭圆的基本量关系、直线垂直的斜率关系求解即可.

    (2)先分析当直线的斜率为0时是否满足，再分析当直线的斜率不为0时，设其方程为，联立椭圆得出韦达定理，再计算可得即可证明.

    （1）因为A为椭圆的上顶点，所以，

    则直线的斜率.

    因为与直线垂直，所以，解得.

    设C的焦距为，因为C的离心率为，所以，.

    则，所以.

    所以C的方程为.

    （2）由（1）知，.

    当直线的斜率为0时，线段即为C的长轴，M或N与B重合，

    则以为直径的圆过点B.

    当直线的斜率不为0时，设其方程为.

    联立，消去x得，

    整理得，设，.

    则，.

    那么

    ，

    所以.

    所以，即以为直径的圆过点B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】千百年来，我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化，总结了丰富的“看云识天气”的经验，并将这些经验编成谚语，如“天上钩钩云，地上雨淋淋”“日落云里走，雨在半夜后”……小波同学为了验证“日落云里走，雨在半夜后”，观察了所在地区的天日落和夜晚天气，得到如下列联表：

    夜晚天气日落云里走

    下雨

    未下雨

    出现

    未出现

    参考公式：.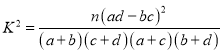

    临界值表：

    （1）根据上面的列联表判断能否有的把握认为“当晚下雨”与“‘日落云里走’出现”有关？

    （2）小波同学为进一步认识其规律，对相关数据进行分析，现从上述调查的“夜晚未下雨”天气中按分层抽样法抽取天，再从这天中随机抽出天进行数据分析，求抽到的这天中仅有天出现“日落云里走”的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

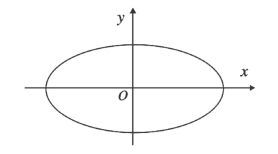
    【题目】已知椭圆的离心率为，且经过点．

    （Ⅰ）求椭圆的标准方程；

    （Ⅱ）设椭圆的上、下顶点分别为， 点是椭圆上异于的任意一点， 轴， 为垂足， 为线段中点，直线交直线于点， 为线段的中点，若四边形的面积为，求直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的图象如图所示，给出四个函数：①，②，③，④，又给出四个函数的图象，则正确的匹配方案是（ ）．

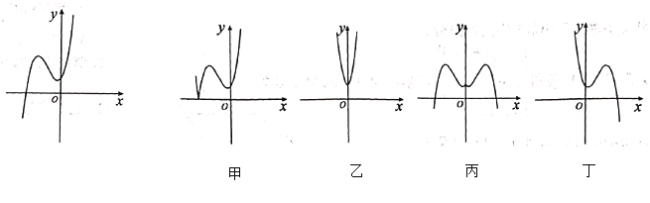
    A.①－甲，②－乙，③－丙，④－丁B.②－甲，①－乙，③－丙，④－丙

    C.①－甲，③－乙，④－丙，②－丁D.①－甲，④－乙，③－丙，②－丁

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知的内角、、的对边分别为、、，且．

    （Ⅰ）求；

    （Ⅱ）若，，如图，为线段上一点，且，求的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】采购经理指数（PMⅠ）是衡量一个国家制造业的“体检表”，是衡量制造业在生产、新订单、商品价格、存货、雇员、订单交货新出口订单和进口等八个方面状况的指数，图为2018年9月—2019年9月我国制造业的采购经理指数（单位：%）．

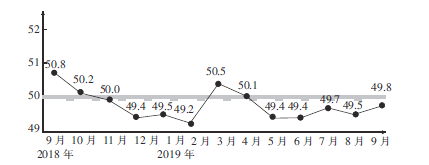
    （1）求2019年前9个月我国制造业的采购经理指数的平均数（精确到0.1）；

    （2）从2018年10月—2019年9月这12个月任意选取4个月，记采购经理指数与上个月相比有所回升的月份个数为X，求X的分布列与期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】学校艺术节对四件参赛作品只评一件一等奖，在评奖揭晓前，甲，乙，丙，丁四位同学对这四件参赛作品预测如下：

    甲说：“是或作品获得一等奖”； 乙说：“ 作品获得一等奖”；

    丙说：“ 两件作品未获得一等奖”； 丁说：“是作品获得一等奖”．

    评奖揭晓后，发现这四位同学中只有两位说的话是对的，则获得一等奖的作品是_________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以平面直角坐标系的原点为极点，轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程为，将曲线绕极点逆时针旋转后得到曲线.

    （Ⅰ）求曲线的极坐标方程；

    （Ⅱ）若直线：与，分别相交于异于极点的，两点，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地一条主于道上有46盏路灯，相邻两盏路灯之间间隔30米，有关部门想在所有相邻路灯间都新添一盏，假设工人每次在两盏灯之间添新路灯是随机，并且每次添新路灯相互独立.新添路灯与左右相邻路灯的间隔都不小于10米是符合要求的，记符合要求的新添路灯数量为，则（ ）

    A.30B.15C.10D.5

    查看答案和解析>>

    同步练习册答案