
°æƒø°ø∑¢’π°∞ª·‘±°±°¢Ã·π©”≈ªð£¨≥…Œ™≤ª…Ÿ µÃµ͑⁄Õ¯π∫≥ª˜œ¬Œ¸“˝øÕ¡˜µƒ÷ÿ“™∑Ω Ω£Æƒ≥¡¨À¯µÍŒ™¡ÀŒ¸“˝ª·‘±£¨‘⁄2019ƒÍ¥∫Ω⁄∆⁄º‰Õ∆≥ˆ“ªœµ¡–”≈ªð¥Ÿœ˙ªÓ∂Ø£Æ≥ÈΩ±∑µœ÷±„ «’Î∂‘°∞∞◊Ωø®ª·‘±°±°¢°∞Ωø®ª·‘±°±°¢°∞“¯ø®ª·‘±°±°¢°∞ª˘±æª·‘±°±≤ªÕ¨º∂±µƒª·‘±œÌ Ð≤ªÕ¨µƒ”≈ªðµƒ“ªœÓªÓ∂Ø£∫°∞∞◊Ωø®ª·‘±°±°¢°∞Ωø®ª·‘±°±°¢°∞“¯ø®ª·‘±°±°¢°∞ª˘±æª·‘±°±∑÷±”–4¥Œ°¢3¥Œ°¢2¥Œ°¢1¥Œ≥ÈΩ±ª˙ª·£Æ≥ÈΩ±ª˙»ÁÕº£∫≥ÈΩ±’þµ⁄“ª¥Œ∞¥œ¬≥ÈΩ±º¸£¨‘⁄’˝Àƒ√Êõƒ∂•µ„![]() ≥ˆœ÷“ª∏ˆ–°«Ú£¨‘Ÿ¥Œ∞¥œ¬≥ÈΩ±º¸£¨–°«Ú“‘œýµ»µƒø…ƒÐ“∆œÚ¡⁄Ω¸µƒ∂•µ„÷Æ“ª£¨‘Ÿ¥Œ∞¥œ¬≥ÈΩ±º¸£¨–°«Ú”÷“‘œýµ»µƒø…ƒÐ“∆œÚ¡⁄Ω¸µƒ∂•µ„÷Æ“ª°≠°≠√ø“ª∏ˆ∂•µ„…œæ˘”–“ª∏ˆ∑¢π‚∆˜£¨–°«Ú‘⁄ƒ≥µ„ ±£¨∏√µ„µ»ø…ƒÐ∑¢∫Ïπ‚ªÚ¿∂π‚£¨»Ù≥ˆœ÷∫Ïπ‚‘ÚªÒµ√2∏ˆµ•Œªœ÷Ω£¨»Ù≥ˆœ÷¿∂π‚‘ÚªÒµ√3∏ˆµ•Œªœ÷Ω£Æ
≥ˆœ÷“ª∏ˆ–°«Ú£¨‘Ÿ¥Œ∞¥œ¬≥ÈΩ±º¸£¨–°«Ú“‘œýµ»µƒø…ƒÐ“∆œÚ¡⁄Ω¸µƒ∂•µ„÷Æ“ª£¨‘Ÿ¥Œ∞¥œ¬≥ÈΩ±º¸£¨–°«Ú”÷“‘œýµ»µƒø…ƒÐ“∆œÚ¡⁄Ω¸µƒ∂•µ„÷Æ“ª°≠°≠√ø“ª∏ˆ∂•µ„…œæ˘”–“ª∏ˆ∑¢π‚∆˜£¨–°«Ú‘⁄ƒ≥µ„ ±£¨∏√µ„µ»ø…ƒÐ∑¢∫Ïπ‚ªÚ¿∂π‚£¨»Ù≥ˆœ÷∫Ïπ‚‘ÚªÒµ√2∏ˆµ•Œªœ÷Ω£¨»Ù≥ˆœ÷¿∂π‚‘ÚªÒµ√3∏ˆµ•Œªœ÷Ω£Æ
£®1£©«Û°∞“¯ø®ª·‘±°±ªÒµ√Ω±Ωµƒ∑÷≤º¡–£ª
£®2£©![]() ±Ì æµ⁄
±Ì æµ⁄![]() ¥Œ∞¥œ¬≥ÈΩ±º¸£¨–°«Ú≥ˆœ÷‘⁄
¥Œ∞¥œ¬≥ÈΩ±º¸£¨–°«Ú≥ˆœ÷‘⁄![]() µ„¥¶µƒ∏≈¬ £Æ
µ„¥¶µƒ∏≈¬ £Æ
¢Ÿ«Û![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() µƒ÷µ£ª
µƒ÷µ£ª
¢⁄–¥≥ˆ![]() ”Î
”Î![]() πÿœµ Ω£¨≤¢Àµ√˜¿Ì”…£Æ
πÿœµ Ω£¨≤¢Àµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©œÍº˚Ω‚Œˆ£ª£®2£©¢Ÿ![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £ª¢⁄
£ª¢⁄![]() £¨¿Ì”…œÍº˚Ω‚Œˆ.
£¨¿Ì”…œÍº˚Ω‚Œˆ.
°æΩ‚Œˆ°ø
£®1£©…Ë°∞“¯ø®ª·‘±°±ªÒµ√Ω±ΩŒ™![]() ∏ˆµ•Œªœ÷Ω£¨µ√≥ˆ
∏ˆµ•Œªœ÷Ω£¨µ√≥ˆ![]() µƒ»°÷µ“‘º∞œý”¶µƒ∏≈¬ £¨◊Ó∫Û¡–≥ˆ∑÷≤º¡–£ª
µƒ»°÷µ“‘º∞œý”¶µƒ∏≈¬ £¨◊Ó∫Û¡–≥ˆ∑÷≤º¡–£ª
£®2£©¢Ÿµ⁄“ª¥Œ∞¥œ¬≥ÈΩ±º¸–°«Ú“ª∂®≥ˆœ÷‘⁄’˝Àƒ√Êõƒ∂•µ„![]() £¨µ√≥ˆ
£¨µ√≥ˆ![]() £¨µ⁄∂˛¥Œ∞¥œ¬ ±£¨–°«Ú“∆œÚ∆‰À¸œý¡⁄µ„£¨‘Ú
£¨µ⁄∂˛¥Œ∞¥œ¬ ±£¨–°«Ú“∆œÚ∆‰À¸œý¡⁄µ„£¨‘Ú![]() £¨µ⁄»˝¥Œ∞¥œ¬ ±£¨”…”⁄–°«Ú≤ª‘⁄µ„
£¨µ⁄»˝¥Œ∞¥œ¬ ±£¨”…”⁄–°«Ú≤ª‘⁄µ„![]() £¨‘Ú
£¨‘Ú![]() £¨µ⁄Àƒ¥Œ∞¥œ¬ ±£¨ø…∑÷¡Ω÷÷«ÈøˆΩ¯––Ã÷¬€£¨µ√≥ˆ
£¨µ⁄Àƒ¥Œ∞¥œ¬ ±£¨ø…∑÷¡Ω÷÷«ÈøˆΩ¯––Ã÷¬€£¨µ√≥ˆ![]() £ª
£ª
¢⁄∑÷¡Ω÷÷«ÈøˆΩ¯––Ã÷¬€£¨µ⁄“ª÷÷£∫µ⁄![]() ¥Œ∞¥œ¬≥ÈΩ±º¸–°«Ú≥ˆœ÷‘⁄
¥Œ∞¥œ¬≥ÈΩ±º¸–°«Ú≥ˆœ÷‘⁄![]() µ„¥¶£¨µ⁄∂˛÷÷£∫µ⁄
µ„¥¶£¨µ⁄∂˛÷÷£∫µ⁄![]() ∞¥œ¬≥ÈΩ±º¸–°«Ú≤ª‘⁄
∞¥œ¬≥ÈΩ±º¸–°«Ú≤ª‘⁄![]() µ„¥¶£¨∏˘æð∂¿¡¢ ¬º˛µƒ–‘÷ £¨º¥ø…µ√≥ˆ
µ„¥¶£¨∏˘æð∂¿¡¢ ¬º˛µƒ–‘÷ £¨º¥ø…µ√≥ˆ![]() ”Î
”Î![]() πÿœµ Ω.
πÿœµ Ω.
£®1£©…Ë°∞“¯ø®ª·‘±°±ªÒµ√Ω±ΩŒ™![]() ∏ˆµ•Œªœ÷Ω£¨‘Ú
∏ˆµ•Œªœ÷Ω£¨‘Ú![]() ø…»°4£¨5£¨6
ø…»°4£¨5£¨6
![]() £ª
£ª![]() £ª
£ª![]()
![]() µƒ∑÷≤º¡–:
µƒ∑÷≤º¡–:
| 4 | 5 | 6 |
|
|
|
|
£®2£©¢Ÿµ⁄“ª¥Œ∞¥œ¬≥ÈΩ±º¸–°«Ú“ª∂®≥ˆœ÷‘⁄’˝Àƒ√Êõƒ∂•µ„![]() £¨µ√≥ˆ
£¨µ√≥ˆ![]()
µ⁄∂˛¥Œ∞¥œ¬ ±£¨–°«Ú“∆œÚ∆‰À¸œý¡⁄µ„£¨‘Ú![]()
µ⁄»˝¥Œ∞¥œ¬ ±£¨”…”⁄–°«Ú≤ª‘⁄µ„![]() £¨‘Ú
£¨‘Ú![]()
µ⁄Àƒ¥Œ∞¥œ¬≥ÈΩ±º¸ ±
»Ùµ⁄»˝¥ŒΩ· ¯–°«Ú‘⁄µ„![]() £¨‘Úµ⁄Àƒ¥Œ∞¥œ¬≥ÈΩ±º¸ ±–°«Ú≥ˆœ÷‘⁄µ„
£¨‘Úµ⁄Àƒ¥Œ∞¥œ¬≥ÈΩ±º¸ ±–°«Ú≥ˆœ÷‘⁄µ„![]() µƒ∏≈¬ Œ™0
µƒ∏≈¬ Œ™0
»Ùµ⁄»˝¥ŒΩ· ¯–°«Ú≤ª‘⁄µ„![]() £¨‘Úµ⁄Àƒ¥Œ∞¥œ¬≥ÈΩ±º¸ ±–°«Ú≥ˆœ÷‘⁄µ„
£¨‘Úµ⁄Àƒ¥Œ∞¥œ¬≥ÈΩ±º¸ ±–°«Ú≥ˆœ÷‘⁄µ„![]() µƒ∏≈¬ Œ™
µƒ∏≈¬ Œ™![]()
![]() £Æ
£Æ
¢⁄”…“‚÷™£∫»Ùµ⁄![]() ¥Œ∞¥œ¬≥ÈΩ±º¸–°«Ú≥ˆœ÷‘⁄
¥Œ∞¥œ¬≥ÈΩ±º¸–°«Ú≥ˆœ÷‘⁄![]() µ„¥¶£¨‘Úµ⁄
µ„¥¶£¨‘Úµ⁄![]() ¥Œ–°«Ú≥ˆœ÷‘⁄
¥Œ–°«Ú≥ˆœ÷‘⁄![]() µ„¥¶µƒ∏≈¬ Œ™0£ª
µ„¥¶µƒ∏≈¬ Œ™0£ª
»Ùµ⁄![]() ∞¥œ¬≥ÈΩ±º¸–°«Ú≤ª‘⁄
∞¥œ¬≥ÈΩ±º¸–°«Ú≤ª‘⁄![]() µ„¥¶£¨‘Úµ⁄
µ„¥¶£¨‘Úµ⁄![]() ¥Œ–°«Ú≥ˆœ÷‘⁄
¥Œ–°«Ú≥ˆœ÷‘⁄![]() µ„¥¶µƒ∏≈¬ Œ™
µ„¥¶µƒ∏≈¬ Œ™![]() £Æ
£Æ
°ý![]() £Æ
£Æ


 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
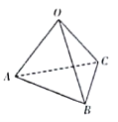
°æƒø°ø“—÷™À´«˙œþ![]() µƒ–È÷·µƒ“ª∏ˆ∂•µ„Œ™
µƒ–È÷·µƒ“ª∏ˆ∂•µ„Œ™![]() £¨◊Û∂•µ„Œ™
£¨◊Û∂•µ„Œ™![]() £¨À´«˙œþ
£¨À´«˙œþ![]() µƒ◊Û°¢”“Ωπµ„∑÷±Œ™
µƒ◊Û°¢”“Ωπµ„∑÷±Œ™![]() £¨
£¨![]() £¨µ„
£¨µ„![]() Œ™œþ∂Œ
Œ™œþ∂Œ![]() …œµƒ∂ص„£¨µ±
…œµƒ∂ص„£¨µ±![]() »°µ√◊Ó–°÷µ∫Õ◊Ó¥Û÷µ ±£¨
»°µ√◊Ó–°÷µ∫Õ◊Ó¥Û÷µ ±£¨![]() µƒ√ʪ˝∑÷±Œ™
µƒ√ʪ˝∑÷±Œ™![]() £¨
£¨![]() £¨»Ù
£¨»Ù![]() £¨‘ÚÀ´«˙œþ
£¨‘ÚÀ´«˙œþ![]() µƒ¿Î–ƒ¬ Œ™£® £©£Æ
µƒ¿Î–ƒ¬ Œ™£® £©£Æ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∂Ø÷±œþ”Î![]() ”ÎÕ÷‘≤
”ÎÕ÷‘≤![]() Ωª”⁄
Ωª”⁄![]() °¢
°¢![]() ¡Ω≤ªÕ¨µ„£¨«“
¡Ω≤ªÕ¨µ„£¨«“![]() µƒ√ʪ˝
µƒ√ʪ˝![]() £¨∆‰÷–
£¨∆‰÷–![]() Œ™◊¯±Í‘≠µ„
Œ™◊¯±Í‘≠µ„
£®1£©»Ù∂Ø÷±œþ![]() ¥π÷±”⁄
¥π÷±”⁄![]() ÷·.«Û÷±œþ
÷·.«Û÷±œþ![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®2£©÷§√˜£∫![]() ∫Õ
∫Õ![]() æ˘Œ™∂®÷µ£ª
æ˘Œ™∂®÷µ£ª
£®3£©Õ÷‘≤![]() …œ «∑ҥʑ⁄µ„
…œ «∑ҥʑ⁄µ„![]() £¨
£¨![]() £¨
£¨![]() £¨ πµ√»˝Ω«–Œ√ʪ˝
£¨ πµ√»˝Ω«–Œ√ʪ˝![]() »Ù¥Ê‘⁄£¨≈–∂œ
»Ù¥Ê‘⁄£¨≈–∂œ![]() µƒ–Œ◊¥£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…
µƒ–Œ◊¥£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™≈◊ŒÔœþ![]() £∫
£∫![]() µƒΩπµ„Œ™
µƒΩπµ„Œ™![]() £¨π˝Ωπµ„◊ˆ«„–±Ω«Œ™µƒ120°„µƒ÷±œþΩª
£¨π˝Ωπµ„◊ˆ«„–±Ω«Œ™µƒ120°„µƒ÷±œþΩª![]() ”⁄
”⁄![]() £¨
£¨![]() ¡Ωµ„£¨
¡Ωµ„£¨![]() Œ™◊¯±Í‘≠µ„£¨
Œ™◊¯±Í‘≠µ„£¨![]() £Æ
£Æ
£®1£©«Û≈◊ŒÔœþ![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®2£©π˝≈◊ŒÔœþΩ𵄣¨«“”Î◊¯±Í÷·≤ª¥π÷±µƒ÷±œþlΩª≈◊ŒÔœþ”⁄![]() £¨
£¨![]() ¡Ωµ„£¨
¡Ωµ„£¨![]() £¨
£¨![]() ‘⁄≈◊ŒÔœþ…œ£¨«“
‘⁄≈◊ŒÔœþ…œ£¨«“![]() £¨
£¨![]() £¨»Ù
£¨»Ù![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() Àƒµ„∂º‘⁄‘≤
Àƒµ„∂º‘⁄‘≤![]() …œ£¨«Û‘≤
…œ£¨«Û‘≤![]() µƒ∑Ω≥ãÆ
µƒ∑Ω≥ãÆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() .
.
£®1£©Ã÷¬€![]() µƒµ•µ˜–‘£ª
µƒµ•µ˜–‘£ª
£®2£©»Ù![]() £¨ ‘≈–∂œ
£¨ ‘≈–∂œ![]() µƒ¡„µ„∏ˆ ˝.
µƒ¡„µ„∏ˆ ˝.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™ ˝¡–![]() ∫Õ
∫Õ![]() µƒ«∞
µƒ«∞![]() œÓ∫Õ∑÷±Œ™
œÓ∫Õ∑÷±Œ™![]() ∫Õ
∫Õ![]() £¨«“
£¨«“![]() £¨
£¨![]() £¨
£¨![]() £¨∆‰÷–
£¨∆‰÷–![]() Œ™≥£ ˝.
Œ™≥£ ˝.
£®1£©»Ù![]() £¨
£¨![]() .
.
¢Ÿ«Û ˝¡–![]() µƒÕ®œÓπ´ Ω£ª
µƒÕ®œÓπ´ Ω£ª
¢⁄«Û ˝¡–![]() µƒÕ®œÓπ´ Ω.
µƒÕ®œÓπ´ Ω.
£®2£©»Ù![]() £¨
£¨![]() .«Û÷§£∫
.«Û÷§£∫![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄÷±»˝¿‚÷˘ABC©ÅA1B1C1÷–£¨AB°ÕBC£¨BB1![]() BC£¨D «CC1µƒ÷–µ„£Æ
BC£¨D «CC1µƒ÷–µ„£Æ

£®1£©÷§√˜£∫B1C°Õ∆Ω√ÊABD£ª
£®2£©»ÙAB£ΩBC£¨E «A1C1µƒ÷–µ„£¨«Û∂˛√ÊΩ«A©ÅBD©ÅEµƒ¥Û–°£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∂®“£∫![]() «ŒÞ«Ó ˝¡–£¨»Ù¥Ê‘⁄’˝’˚ ˝k πµ√∂‘»Œ“‚
«ŒÞ«Ó ˝¡–£¨»Ù¥Ê‘⁄’˝’˚ ˝k πµ√∂‘»Œ“‚![]() £¨æ˘”–
£¨æ˘”–![]() ‘Ú≥∆
‘Ú≥∆![]() «Ω¸À∆µð‘ˆ£®ºı£© ˝¡–£¨∆‰÷–kΩ–Ω¸À∆µð‘ˆ£®ºı£© ˝¡–
«Ω¸À∆µð‘ˆ£®ºı£© ˝¡–£¨∆‰÷–kΩ–Ω¸À∆µð‘ˆ£®ºı£© ˝¡–![]() µƒº‰∏Ù ˝
µƒº‰∏Ù ˝
£®1£©»Ù![]() £¨
£¨![]() «≤ª «Ω¸À∆µð‘ˆ ˝¡–£¨≤¢Àµ√˜¿Ì”…
«≤ª «Ω¸À∆µð‘ˆ ˝¡–£¨≤¢Àµ√˜¿Ì”…
£®2£©“—÷™ ˝¡–![]() µƒÕ®œÓπ´ ΩŒ™
µƒÕ®œÓπ´ ΩŒ™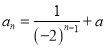 £¨∆‰«∞nœÓµƒ∫ÕŒ™
£¨∆‰«∞nœÓµƒ∫ÕŒ™![]() £¨»Ù2 «Ω¸À∆µð‘ˆ ˝¡–
£¨»Ù2 «Ω¸À∆µð‘ˆ ˝¡–![]() µƒº‰∏Ù ˝£¨«Ûaµƒ»°÷µ∑∂Œß£∫
µƒº‰∏Ù ˝£¨«Ûaµƒ»°÷µ∑∂Œß£∫
£®3£©“—÷™![]() £¨÷§√˜
£¨÷§√˜![]() «Ω¸À∆µðºı ˝¡–£¨≤¢«“4 «À¸µƒ◊Ó–°º‰∏Ù ˝.
«Ω¸À∆µðºı ˝¡–£¨≤¢«“4 «À¸µƒ◊Ó–°º‰∏Ù ˝.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥…Ã≥°Ω¯––≥ÈΩ±¥Ÿœ˙ªÓ∂Ø£¨≥ÈΩ±œ‰÷–”–¥Û–°ÕÍ»´œýÕ¨µƒ4∏ˆ–°«Ú£¨∑÷±±Í”–°∞A°±°∞B°±°∞C°±°∞D°±.πÀøÕ¥”÷–»Œ“‚»°≥ˆ1∏ˆ«Ú£¨º«œ¬…œ√ʵƒ◊÷∫Û∑≈ªÿœ‰÷–£¨‘Ÿ¥”÷–»Œ»°1∏ˆ«Ú£¨÷ÿ∏¥“‘…œ≤Ÿ◊˜£¨◊Ó∂ý»°4¥Œ£¨≤¢πÊ∂®»Ù»°≥ˆ°∞D°±◊÷«Ú£¨‘ÚÕ£÷π»°«Ú.ªÒΩ±πÊ‘Ú»Áœ¬£∫“¿¥Œ»°µΩ±Í”–°∞°∞A°±°∞B°±°∞C°±°∞D°±◊÷µƒ«ÚŒ™“ªµ»Ω±£ª≤ª∑÷À≥–Ú»°µΩ±Í”–°∞A°±°∞B°±°∞C°±°∞D°±◊÷µƒ«Ú£¨Œ™∂˛µ»Ω±£ª»°µΩµƒ4∏ˆ«Ú÷–”–±Í”–°∞A°±°∞B°±°∞C°±»˝∏ˆ◊÷µƒ«ÚŒ™»˝µ»Ω±.
£®1£©«Û∑÷±ªÒµ√“ª°¢∂˛°¢»˝µ»Ω±µƒ∏≈¬ £ª
£®2£©…Ë√˛«Ú¥Œ ˝Œ™![]() £¨«Û
£¨«Û![]() µƒ∑÷≤º¡–∫Õ ˝—ß∆⁄Õ˚.
µƒ∑÷≤º¡–∫Õ ˝—ß∆⁄Õ˚.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com