
【题目】定义:![]() 是无穷数列,若存在正整数k使得对任意
是无穷数列,若存在正整数k使得对任意![]() ,均有
,均有![]() 则称
则称![]() 是近似递增(减)数列,其中k叫近似递增(减)数列
是近似递增(减)数列,其中k叫近似递增(减)数列![]() 的间隔数
的间隔数
(1)若![]() ,
,![]() 是不是近似递增数列,并说明理由
是不是近似递增数列,并说明理由
(2)已知数列![]() 的通项公式为
的通项公式为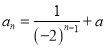 ,其前n项的和为
,其前n项的和为![]() ,若2是近似递增数列
,若2是近似递增数列![]() 的间隔数,求a的取值范围:
的间隔数,求a的取值范围:
(3)已知![]() ,证明
,证明![]() 是近似递减数列,并且4是它的最小间隔数.
是近似递减数列,并且4是它的最小间隔数.
【答案】(1)是近似递增数列,详见解析(2)![]() (3)证明见解析;
(3)证明见解析;
【解析】
(1)根据近似递增数列的定义判断可知![]() 是近似递增数列;
是近似递增数列;
(2)求出![]() ,根据
,根据![]() ,即
,即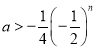 恒成立,可得
恒成立,可得![]() ;
;
(3)因为![]() 等价于
等价于![]() ,因为n,k是正整数,所以
,因为n,k是正整数,所以![]() ,
,![]() 均取不到
均取不到![]() ,所以
,所以![]() 时上式恒成立,可得
时上式恒成立,可得![]() 是近似递减数列,再验证
是近似递减数列,再验证![]() 时,
时,![]() 不是近似递减数列,则可得4是它的最小间隔数.
不是近似递减数列,则可得4是它的最小间隔数.
(1)是近似递增数列,理由如下:
因为![]() ,
,
或![]() [注:2,3,4,…,都是间隔数.]
[注:2,3,4,…,都是间隔数.]
即![]() ,所以
,所以![]() 是近似递增数列.
是近似递增数列.
(2)由题意得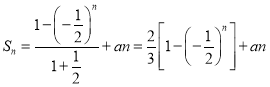 ,
,
所以![]()
![]()
![]()
![]() 对任意
对任意![]() 恒成立,
恒成立,
即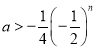 恒成立,.
恒成立,.
令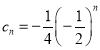 ,则
,则![]() ,
,
即a的取值范围是![]() .
.
(3)因为![]() 等价于
等价于![]() ,
,
即![]() ,(*)
,(*)
因为n,k是正整数,所以![]() ,
,![]() 均取不到
均取不到![]() ,
,
所以![]() 时上式恒成立,即
时上式恒成立,即![]() 是近似递减数列,4是它的间隔数.
是近似递减数列,4是它的间隔数.
当![]() ,当
,当![]() 时,
时,![]() ,故不等式(*)不成立;
,故不等式(*)不成立;
当![]() ,当
,当![]() 时,
时,![]() ,故不等式(*)不成立;
,故不等式(*)不成立;
当![]() ,当
,当![]() 时,
时,![]() ,故不等式(*)不成立;
,故不等式(*)不成立;
所以,4是它的最小间隔数.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为![]() (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为![]() (θ为参数).
(θ为参数).
(1)当![]() 时,求直线l与曲线C的普通方程;
时,求直线l与曲线C的普通方程;
(2)若直线l与曲线C交于A,B两点,直线l倾斜角的范围为(0,![]() ],且P点的直角坐标为(0,2),求
],且P点的直角坐标为(0,2),求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】发展“会员”、提供优惠,成为不少实体店在网购冲击下吸引客流的重要方式.某连锁店为了吸引会员,在2019年春节期间推出一系列优惠促销活动.抽奖返现便是针对“白金卡会员”、“金卡会员”、“银卡会员”、“基本会员”不同级别的会员享受不同的优惠的一项活动:“白金卡会员”、“金卡会员”、“银卡会员”、“基本会员”分别有4次、3次、2次、1次抽奖机会.抽奖机如图:抽奖者第一次按下抽奖键,在正四面体的顶点![]() 出现一个小球,再次按下抽奖键,小球以相等的可能移向邻近的顶点之一,再次按下抽奖键,小球又以相等的可能移向邻近的顶点之一……每一个顶点上均有一个发光器,小球在某点时,该点等可能发红光或蓝光,若出现红光则获得2个单位现金,若出现蓝光则获得3个单位现金.
出现一个小球,再次按下抽奖键,小球以相等的可能移向邻近的顶点之一,再次按下抽奖键,小球又以相等的可能移向邻近的顶点之一……每一个顶点上均有一个发光器,小球在某点时,该点等可能发红光或蓝光,若出现红光则获得2个单位现金,若出现蓝光则获得3个单位现金.
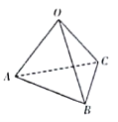
(1)求“银卡会员”获得奖金的分布列;
(2)![]() 表示第
表示第![]() 次按下抽奖键,小球出现在
次按下抽奖键,小球出现在![]() 点处的概率.
点处的概率.
①求![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
②写出![]() 与
与![]() 关系式,并说明理由.
关系式,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是2020年2月15日至3月2日武汉市新增新冠肺炎确诊病例的折线统计图.则下列说法不正确的是( )

A.2020年2月19日武汉市新增新冠肺炎确诊病例大幅下降至三位数
B.武汉市在新冠肺炎疫情防控中取得了阶段性的成果,但防控要求不能降低
C.2020年2月19日至3月2日武汉市新增新冠肺炎确诊病例低于400人的有8天
D.2020年2月15日到3月2日武汉市新增新冠肺炎确诊病例最多的一天比最少的一天多1549人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形![]() 中,
中,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,
上的点,![]() ,且
,且![]() (如图①).将四边形
(如图①).将四边形![]() 沿
沿![]() 折起,连接
折起,连接![]() 、
、![]() 、
、![]() (如图②).在折起的过程中,则下列表述:
(如图②).在折起的过程中,则下列表述:

①![]() 平面
平面![]() ;
;
②四点![]() 、
、![]() 、
、![]() 、
、![]() 可能共面;
可能共面;
③若![]() ,则平面
,则平面![]() 平面
平面![]() ;
;
④平面![]() 与平面
与平面![]() 可能垂直.其中正确的是__________.
可能垂直.其中正确的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是![]() 的中点.
的中点.
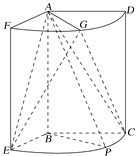
(1)设P是![]() 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;
(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冠状病毒是一个大型病毒家族,已知可引起感冒以及中东呼吸综合征![]() 和严重急性呼吸综合征
和严重急性呼吸综合征![]() 等较严重疾病.而今年初出现并在全球蔓延的新型冠状病毒
等较严重疾病.而今年初出现并在全球蔓延的新型冠状病毒![]() 是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.
是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.
某药物研究所为筛查该种病毒,需要检验血液是否为阳性,现有![]() (
(![]() ,且
,且![]() )份血液样本,每个样本取到的可能性相等,有以下两种检验方式:
)份血液样本,每个样本取到的可能性相等,有以下两种检验方式:
方式一:逐份检验则需要检验![]() 次;
次;
方式二:混合检验,将![]() 份血液样本分别取样混合在一起检验,若检验结果为阴性,则这
份血液样本分别取样混合在一起检验,若检验结果为阴性,则这![]() 份的血液全为阴性,因而这
份的血液全为阴性,因而这![]() 份血液样本只要检验一次就够了;如果检验结果为阳性,为了明确这
份血液样本只要检验一次就够了;如果检验结果为阳性,为了明确这![]() 份血液究竟哪几份为阳性,就要对这
份血液究竟哪几份为阳性,就要对这![]() 份再逐份检验,此时这
份再逐份检验,此时这![]() 份血液的检验次数总共为
份血液的检验次数总共为![]() 次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为![]() .
.
(1)假设有6份血液样本,其中只有2份样本为阳性,从中任取3份样本进行医学研究,求至少有1份为阳性样本的概率;
(2)假设将![]() (
(![]() 且
且![]() )份血液样本进行检验,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本进行检验,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() ;
;
①运用概率统计的知识,若![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
②若![]() 与干扰素计量
与干扰素计量![]() 相关,其中数列
相关,其中数列![]() 满足
满足![]() ,当
,当![]() 时,试讨论采用何种检验方式更好?
时,试讨论采用何种检验方式更好?
参考数据:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com