
【题目】在直角梯形ABCD中(如图1),![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点E在CD上,且
,点E在CD上,且![]() ,将
,将![]() 沿AE折起,使得平面
沿AE折起,使得平面![]() 平面ABCE(如图2),G为AE中点.
平面ABCE(如图2),G为AE中点.

(Ⅰ)求四棱锥![]() 的体积;
的体积;
(Ⅱ)在线段BD上是否存在点P,使得![]() 平面ADE?若存在,求
平面ADE?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(Ⅰ)![]() (Ⅱ)存在,
(Ⅱ)存在,![]()
【解析】
(Ⅰ)根据平面与平面垂直的性质定理得到![]() 平面ABCE,再根据椎体的体积公式计算可得结果;
平面ABCE,再根据椎体的体积公式计算可得结果;
(Ⅱ)过点C作![]() 交AB于点F,过点F作
交AB于点F,过点F作![]() 交DB于点P,连接PC,可证得平面
交DB于点P,连接PC,可证得平面![]() 平面ADE,再根据平面与平面平行的性质可得
平面ADE,再根据平面与平面平行的性质可得![]() 平面ADE,最后根据平面几何知识可求得比值.
平面ADE,最后根据平面几何知识可求得比值.
(Ⅰ)证明:因为G为AE中点,![]() ,所以
,所以![]() .
.
因为平面![]() 平面ABCE,平面
平面ABCE,平面![]() 平面
平面![]() ,
,
![]() 平面ADE,所以
平面ADE,所以![]() 平面ABCE.
平面ABCE.
在直角三角形ADE中,易求![]() ,
,
则![]() ,
,
所以四棱锥![]() 的体积
的体积![]() .
.
(Ⅱ)在BD上存在点P,使得![]() 平面ADE且
平面ADE且![]() ,
,
过点C作![]() 交AB于点F,过点F作
交AB于点F,过点F作![]() 交DB于点P,连接PC,
交DB于点P,连接PC,
如图所示:
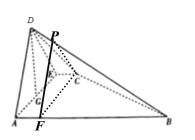
因为![]() ,
,![]() 平面ADE.
平面ADE.![]() 平面ADE,所以
平面ADE,所以![]() 平面ADE,
平面ADE,
同理![]() 平面ADE,
平面ADE,
又因为![]() ,所以平面
,所以平面![]() 平面ADE.
平面ADE.
因为![]() 平面CFP,所以
平面CFP,所以![]() 平面ADE.
平面ADE.
所以在BD上存在点P,使得![]() 平面ADE.
平面ADE.
因为四边形AECF为平行四边形.
所以![]() ,即
,即![]() ,
,
故![]() .
.
所以在BD上存在点P,使得![]() 平面ADE且
平面ADE且![]() .
.


科目:高中数学 来源: 题型:
【题目】在一个不透明的盒子中装有4个大小、形状、手感完全相同的小球,分别标有数字1,2,3,4.现每次有放回地从中任意取出一个小球,直到标有偶数的球都取到过就停止.小明用随机模拟的方法估计恰好在第3次停止摸球的概率,利用计算机软件产生随机数,每1组中有3个数字,分别表示每次摸球的结果,经随机模拟产生了以下18组随机数:
131 432 123 233 234 122 332 141 312 241 122 214 431 241 141 433 223 442
由此可以估计恰好在第3次停止摸球的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为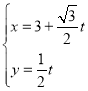 (
(![]() 为参数),在以坐标原点
为参数),在以坐标原点![]() 为极点、以
为极点、以![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求线段![]() 的中点
的中点![]() 的直角坐标;
的直角坐标;
(2)设点![]() 是曲线
是曲线![]() 上任意一点,求
上任意一点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为![]() 内角A,B,C的对边,若
内角A,B,C的对边,若![]() 同时满足以下四个条件中的三个:①
同时满足以下四个条件中的三个:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
(1)条件①②能否同时满足,请说明理由;
(2)以上四个条件,请在满足三角形有解的所有组合中任选一组,并求出对应![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是2020项的实数数列,
是2020项的实数数列,![]() 中的每一项都不为零,
中的每一项都不为零,![]() 中任意连续11项
中任意连续11项![]() 的乘积是定值
的乘积是定值![]() .
.
①存在满足条件的数列,使得其中恰有365个1;
②不存在满足条件的数列,使得其中恰有550个1.
命题的真假情况为( )
A.①和②都是真命题B.①是真命题,②是假命题
C.②是真命题,①是假命题D.①和②都是假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“众志成城,抗击疫情,一方有难,八方支援”,在此次抗击疫情过程中,各省市都派出援鄂医疗队. 假设汕头市选派![]() 名主任医生,
名主任医生,![]() 名护士,组成三个医疗小组分配到湖北甲、乙、丙三地进行医疗支援,每个小组包括
名护士,组成三个医疗小组分配到湖北甲、乙、丙三地进行医疗支援,每个小组包括![]() 名主任医生和
名主任医生和![]() 名护士,则不同的分配方案有( )
名护士,则不同的分配方案有( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率为
的离心率为![]() ,左焦点
,左焦点![]() 到直线
到直线![]() 的距离为10,圆
的距离为10,圆![]() .
.
(1)求椭圆的方程;
(2)若![]() 是椭圆上任意一点,
是椭圆上任意一点,![]() 为圆
为圆![]() 的任一直径,求
的任一直径,求![]() 的取值范围;
的取值范围;
(3)是否存在以椭圆上点![]() 为圆心的圆
为圆心的圆![]() ,使得过圆
,使得过圆![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的切线,切点为
的切线,切点为![]() ,都满足
,都满足![]() ?若存在,求出圆
?若存在,求出圆![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,对于函数
,对于函数![]() 有下述四个结论:
有下述四个结论:
①函数![]() 在其定义域上为增函数;
在其定义域上为增函数;
②对于任意的![]() ,都有
,都有![]() 成立;
成立;
③![]() 有且仅有两个零点;
有且仅有两个零点;
④若![]() 在点
在点![]() 处的切线也是
处的切线也是![]() 的切线,则
的切线,则![]() 必是
必是![]() 零点.
零点.
其中所有正确的结论序号是( )
A.①②③B.①②C.②③④D.②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com