
【题目】若二次函数g(x)=ax2+bx+c(a≠0)满足g(x+1)=2x+g(x),且g(0)=1.
(1)求g(x)的解析式;
(2)若在区间[-1,1]上,不等式g(x)-t>2x恒成立,求实数t的取值范围.
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】东西向的铁路上有两个道口![]() 、
、![]() ,铁路两侧的公路分布如图,
,铁路两侧的公路分布如图,![]() 位于
位于![]() 的南偏西
的南偏西![]() ,且位于
,且位于![]() 的南偏东
的南偏东![]() 方向,
方向,![]() 位于
位于![]() 的正北方向,
的正北方向,![]() ,
,![]() 处一辆救护车欲通过道口前往
处一辆救护车欲通过道口前往![]() 处的医院送病人,发现北偏东
处的医院送病人,发现北偏东![]() 方向的
方向的![]() 处(火车头位置)有一列火车自东向西驶来,若火车通过每个道口都需要
处(火车头位置)有一列火车自东向西驶来,若火车通过每个道口都需要![]() 分钟,救护车和火车的速度均为
分钟,救护车和火车的速度均为![]() .
.
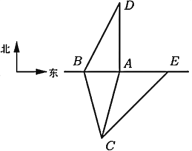
(1)判断救护车通过道口![]() 是否会受火车影响,并说明理由;
是否会受火车影响,并说明理由;
(2)为了尽快将病人送到医院,救护车应选择![]() 、
、![]() 中的哪个道口?通过计算说明.
中的哪个道口?通过计算说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某湿地公园的鸟瞰图是一个直角梯形,其中:![]() ,
,![]() ,
,![]() ,
,![]() 长1千米,
长1千米,![]() 长
长![]() 千米,公园内有一个形状是扇形的天然湖泊
千米,公园内有一个形状是扇形的天然湖泊![]() ,扇形
,扇形![]() 以
以![]() 长为半径,弧
长为半径,弧![]() 为湖岸,其余部分为滩地,B,D点是公园的进出口.公园管理方计划在进出口之间建造一条观光步行道:线段
为湖岸,其余部分为滩地,B,D点是公园的进出口.公园管理方计划在进出口之间建造一条观光步行道:线段![]() 线段
线段![]() 弧
弧![]() ,其中Q在线段
,其中Q在线段![]() 上(异于线段端点),
上(异于线段端点),![]() 与弧
与弧![]() 相切于P点(异于弧端点]根据市场行情
相切于P点(异于弧端点]根据市场行情![]() ,
,![]() 段的建造费用是每千米10万元,湖岸段弧
段的建造费用是每千米10万元,湖岸段弧![]() 的建造费用是每千米
的建造费用是每千米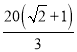 万元(步行道的宽度不计),设
万元(步行道的宽度不计),设![]() 为
为![]() 弧度观光步行道的建造费用为
弧度观光步行道的建造费用为![]() 万元.
万元.
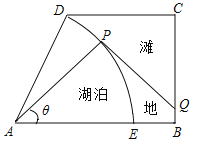
(1)求步行道的建造费用![]() 关于
关于![]() 的函数关系式,并求其走义域;
的函数关系式,并求其走义域;
(2)当![]() 为何值时,步行道的建造费用最低?
为何值时,步行道的建造费用最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,
,![]() 且椭圆上存在一点P,满足.
且椭圆上存在一点P,满足.![]() ,
,![]()
(1)求椭圆C的标准方程;
(2)已知A,B分别是椭圆C的左、右顶点,过![]() 的直线交椭圆C于M,N两点,记直线
的直线交椭圆C于M,N两点,记直线![]() ,
,![]() 的交点为T,是否存在一条定直线l,使点T恒在直线l上?
的交点为T,是否存在一条定直线l,使点T恒在直线l上?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=![]() ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
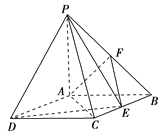
(1)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(2)求证:无论点E在BC边的何处,都有![]() ;
;
(3)当![]() 为何值时,
为何值时,![]() 与平面
与平面![]() 所成角的大小为45°.
所成角的大小为45°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣1|﹣a.
(1)当a=1时,解不等式f(x)>x+1;
(2)若存在实数x,使得f(x)![]() f(x+1),求实数a的取值范围.
f(x+1),求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com