练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图所示，在正三角形ABC中，D，E分别在AC，AB上，且＝，AE＝BE，则有

    A．△AED∽△BED
    B．△AED∽△CBD
    C．△AED∽△ABD
    D．△BAD∽△BCD

    B

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    （本小题满分10分）选修4-4：坐标系与参数方程
    已知曲线。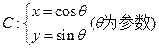
    （Ⅰ）将曲线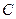的参数方程化为普通方程；
    （Ⅱ）若把曲线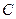上各点的坐标经过伸缩变换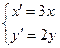后得到曲线，求曲线上任意一点到两坐标轴距离之积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    如图，是圆的内接三角行，的平分线交圆于点D，交BC于E，过点B的圆的切线与AD的延长线交于点F，在上述条件下，给出下列四个结论：①BD平分；②；③；④.则所有正确结论的序号是（   ）

    A．①② B．③④ C．①②③ D．①②④

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    如图所示，圆内接四边形ABCD的一组对边AD、BC的延长线相交于点P，对角线AC、BD相交于点Q，则图中相似三角形共有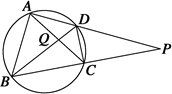

    A．4对    B．2对    C．5对    D．3对

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    如图所示，四边形ABCD是⊙O的内接四边形，延长BC到E，已知∠BCD∶∠ECD＝3∶2，那么∠BOD等于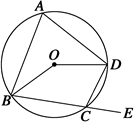

    A．120° B．136°
    C．144° D．150°

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    如图所示，PA切圆于A，PA＝8，直线PCB交圆于C、B，连接AB、AC，且PC＝4，AD⊥BC于D，∠ABC＝α，∠ACB＝β，则的值等于

    A.      B.      C．2      D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    如图所示，点D、E分别在AB、AC上，下列条件能判定△ADE与△ACB相似的有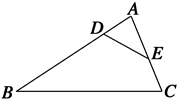
    ①∠AED＝∠B
    ②＝
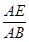
    ③＝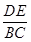
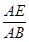
    ④DE∥BC
    A．1个   B．2个   C．3个   D．4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    在△ABC中，∠BAC＝90°，AD是BC边上的高，则相似三角形共有

    A．0对 B．1对 C．2对 D．3对

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知，如图，在梯形ABCD中，AD//BC，AD=3，BC=7，点M，N分别是
    对角线BD，AC的中点，则MN="          "

    A．2 B． 5 C． D．

    查看答案和解析>>

    同步练习册答案