
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)若![]() ,且
,且![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的最大值;
的最大值;
(Ⅲ)当![]() 时,证明:
时,证明:![]() .
.
【答案】(Ⅰ)![]() ;(II)3;(Ⅲ)证明见解析.
;(II)3;(Ⅲ)证明见解析.
【解析】
(Ⅰ)求出![]() 的值,可得切线斜率,利用点斜式可得曲线
的值,可得切线斜率,利用点斜式可得曲线![]() 在点
在点![]() 处的切线方程;(Ⅱ)
处的切线方程;(Ⅱ)![]() 对任意
对任意![]() 恒成立,等价于
恒成立,等价于![]() 对任意
对任意![]() 恒成立,
恒成立,![]() ,利用导数求得
,利用导数求得![]() ,从而可求整数
,从而可求整数![]() 的最大值;(Ⅲ)由(Ⅱ)知,
的最大值;(Ⅲ)由(Ⅱ)知,![]() 是
是![]() 上的增函数, 当
上的增函数, 当![]() 时,
时,![]() ,利用对数的运算结合
,利用对数的运算结合![]() ,化简即可得结论.
,化简即可得结论.
(Ⅰ)![]() ,
,
函数![]() 的图象在点
的图象在点![]() 处的切线方程
处的切线方程![]() ;
;
(Ⅱ)由(Ⅰ)知,![]() ,对任意
,对任意![]() 恒成立,
恒成立,
即![]() 对任意
对任意![]() 恒成立.
恒成立.
令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
所以函数![]() 在
在![]() 上单调递增.
上单调递增.
![]() ,
,
![]() 方程
方程![]() 在
在![]() 上存在唯一实根
上存在唯一实根![]() ,且满足
,且满足![]() .
.
当![]() 时,
时,![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
![]() ,
,
![]() ,
,
故整数![]() 的最大值是3.
的最大值是3.
(Ⅲ)由(Ⅱ)知,![]() 是
是![]() 上的增函数,
上的增函数,
![]() 当
当![]() 时,
时,![]() .
.
即![]() .
.
整理,得![]() .
.
![]() .
.
即![]() .
.
即![]() .
.
![]() .
.


科目:高中数学 来源: 题型:
【题目】某单位有4位同事各有一辆私家车,车牌尾数分别是0,1,2,5,为遵守所在城市元月15日至18日4天的限行规定(奇数日车牌尾数为奇数的车通行,偶数日车牌尾数为偶数的车通行),四人商议拼车出行,每天任选一辆符合规定的车,但甲的车(车牌尾数为2)最多只能用一天,则不同的用车方案种数是( )
A.4B.12C.16D.24
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点 和点
和点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在长方体ABCD﹣A1B1C1D1,若AB=BC,E,F分别是AB1,BC1的中点,则下列结论中不成立的是( )

A.EF与BB1垂直B.EF⊥平面BDD1B1
C.EF与C1D所成的角为45°D.EF∥平面A1B1C1D1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现代社会,“鼠标手”已成为常见病,一次实验中,10名实验对象进行160分钟的连续鼠标点击游戏,每位实验对象完成的游戏关卡一样,鼠标点击频率平均为180次/分钟,实验研究人员测试了实验对象使用鼠标前后的握力变化,前臂表面肌电频率(![]() )等指标.
)等指标.
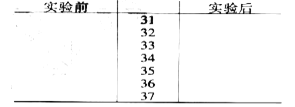
(I)10 名实验对象实验前、后握力(单位:![]() )测试结果如下:
)测试结果如下:
实验前:346,357,358,360,362,362,364,372,373,376
实验后:313,321,322,324,330,332,334,343,350,361
完成茎叶图,并计算实验后握力平均值比实验前握力的平均值下降了多少![]() ?
?
(Ⅱ)实验过程中测得时间![]() (分)与10名实验对象前臂表面肌电频率(
(分)与10名实验对象前臂表面肌电频率(![]() )的中的位数
)的中的位数![]() (
(![]() )的九组对应数据
)的九组对应数据![]() 为
为![]() ,
,![]() .建立
.建立![]() 关于时间
关于时间![]() 的线性回归方程;
的线性回归方程;
(Ⅲ)若肌肉肌电水平显著下降,提示肌肉明显进入疲劳状态,根据(Ⅱ)中9组数据分析,使用鼠标多少分钟就该进行休息了?
参考数据:![]() ;
;
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
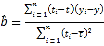 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,近日我渔船编队在岛![]() 周围海域作业,在岛
周围海域作业,在岛![]() 的南偏西20°方向有一个海面观测站
的南偏西20°方向有一个海面观测站![]() ,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与
,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与![]() 相距31海里的
相距31海里的![]() 处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛
处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛![]() 直线航行以保护我渔船编队,30分钟后到达
直线航行以保护我渔船编队,30分钟后到达![]() 处,此时观测站测得
处,此时观测站测得![]() 间的距离为21海里.
间的距离为21海里.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)试问海警船再向前航行多少分钟方可到岛![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为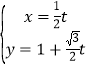 (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 且
且![]() ).
).
(I)求直线![]() 的极坐标方程及曲线
的极坐标方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知![]() 是直线
是直线![]() 上的一点,
上的一点,![]() 是曲线
是曲线![]() 上的一点,
上的一点, ![]() ,
,![]() ,若
,若![]() 的最大值为2,求
的最大值为2,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com