练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数.

    （1）若曲线在点处的切线方程是，求函数在上的值域；

    （2）当时，记函数，若函数有三个零点，求实数的取值范围.

    【答案】（1）； （2）.

    【解析】

    （1）因为，

    所以，所以，

    所以，即.

    ，，，

    所以在上的值域为.

    （2）（i）当时，，由，得，此时函数有三个零点，符合题意.

    （ii）当时，.由，得.当时，；当时，.若函数有三个零点，则需满足且，解得.

    （iii）当时，.由，得，.

    ①当，即时，因为，此时函数至多有一个零点，不符合题意；

    ②当，即时，因为，此时函数至多有两个零点，不符合题意；

    ③当，即时，

    若，函数至多有两个零点，不符题意；

    若，得，因为，所以，此时函数有三个零点，符合题意；

    若，得，由，记，则，所以，此时函数有四个零点，不符合题意.

    综上所述：满足条件的实数.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】随着城市地铁建设的持续推进，市民的出行也越来越便利．根据大数据统计，某条地铁线路运行时，发车时间间隔t（单位：分钟）满足：4≤t≤15，N，平均每趟地铁的载客人数p(t)（单位：人）与发车时间间隔t近似地满足下列函数关系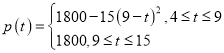：，其中.

    (1）若平均每趟地铁的载客人数不超过1500人，试求发车时间间隔t的值．

    (2）若平均每趟地铁每分钟的净收益为（单位：元），问当发车时间间隔t为多少时，平均每趟地铁每分钟的净收益最大？井求出最大净收益．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】东方商店欲购进某种食品（保质期两天），此商店每两天购进该食品一次（购进时，该食品为刚生产的）.根据市场调查，该食品每份进价元，售价元，如果两天内无法售出，则食品过期作废，且两天内的销售情况互不影响，为了了解市场的需求情况，现统计该产品在本地区天的销售量如下表：

    （视样本频率为概率）

    （1）根据该产品天的销售量统计表，记两天中一共销售该食品份数为，求的分布列与期望

    （2）以两天内该产品所获得的利润期望为决策依据，东方商店一次性购进或份，哪一种得到的利润更大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右顶点分别为，，上下顶点分别为，，左、右焦点分别为，，离心率为e.

    （1）若，设四边形的面积为，四边形的面积为，且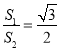，求椭圆C的方程；

    （2）若，设直线与椭圆C相交于P，Q两点，分别为线段，的中点，坐标原点O在以MN为直径的圆上，且，求实数k的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，圆的参数方程为（为参数），以直角坐标系的原点为极点，轴正半轴为极轴建立极坐标系.

    （1）求圆的极坐标方程；

    （2）设曲线的极坐标方程为，曲线的极坐标方程为，求三条曲线，，所围成图形的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在棱长为a的正方体ABCD-A1B1C1D1中，E是棱DD1的中点：

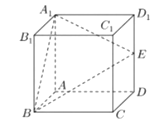
    (1)求点D到平面A1BE的距离；

    (2)在棱上是否存在一点F，使得B1F∥平面A1BE，若存在，指明点F的位置；若不存在，请说明理由。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】折纸与数学有着千丝万缕的联系，吸引了人们的广泛兴趣．因纸的长宽比称为白银分割比例，故纸有一个白银矩形的美称．现有一张如图1所示的纸，．

    分别为的中点，将其按折痕折起（如图2），使得四点重合，重合后的点记为，折得到一个如图3所示的三棱锥．记为的中点，在中，为边上的高．

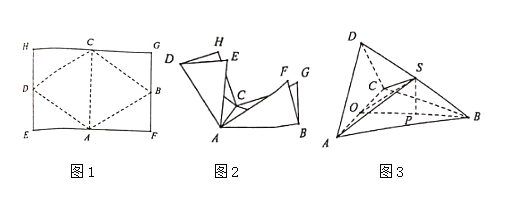
    （1）求证：平面；

    （2）若分别是棱上的动点，且．当三棱锥的体积最大时，求平面与平面所成锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（注意：在试题卷上作答无效）

    已知数列中，.

    （Ⅰ）设，求数列的通项公式；

    （Ⅱ）求使不等式成立的的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设抛物线C：y2＝4x的焦点为F，过F的直线l与C交于A，B两点，点M的坐标为（﹣1，0）.

    （1）当l与x轴垂直时，求△ABM的外接圆方程；

    （2）记△AMF的面积为S1，△BMF的面积为S2，当S1＝4S2时，求直线l的方程.

    查看答案和解析>>

    同步练习册答案