
【题目】已知各项均大于1的数列{an}满足:a1= ![]() ,an+1=
,an+1= ![]() (an+
(an+ ![]() ),(n∈N*),bn=log5
),(n∈N*),bn=log5 ![]() .
.
(1)证明{bn}为等比数列,并求{bn}通项公式;
(2)若cn= ![]() ,Tn为{cn}的前n项和,求证:Tn<6.
,Tn为{cn}的前n项和,求证:Tn<6.
【答案】
(1)证明:由an+1= ![]() (an+
(an+ ![]() ),可得:
),可得:
bn+1=log5 ![]() =log5
=log5  =log5(
=log5( ![]() )2=2log5
)2=2log5 ![]() ,
,
即有 ![]() =
= 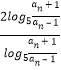 =2,
=2,
则{bn}是首项为b1=log5 ![]() =1,公比为2的等比数列;
=1,公比为2的等比数列;
且bn=b1qn﹣1=2n﹣1;
(2)证明:cn= ![]() =
= ![]() =(n+1)(
=(n+1)( ![]() )n﹣1,
)n﹣1,
可得Tn=21+3 ![]() +4(
+4( ![]() )2+…+(n+1)(
)2+…+(n+1)( ![]() )n﹣1,
)n﹣1,
![]() Tn=2
Tn=2 ![]() +3(
+3( ![]() )2+4(
)2+4( ![]() )3+…+(n+1)(
)3+…+(n+1)( ![]() )n,
)n,
两式相减可得, ![]() Tn=2+[
Tn=2+[ ![]() +(
+( ![]() )2+(
)2+( ![]() )3+…+(
)3+…+( ![]() )n﹣1]﹣(n+1)(
)n﹣1]﹣(n+1)( ![]() )n
)n
=2+ 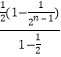 ﹣(n+1)(
﹣(n+1)( ![]() )n=3﹣
)n=3﹣ ![]() ﹣
﹣ ![]() ,
,
则Tn=6﹣ ![]() <6成立.
<6成立.
【解析】(1)运用对数的运算性质,结合等比数列的定义,可得 ![]() =2,即可得证,再由等比数列的通项公式即可得到所求;(2)求得cn=
=2,即可得证,再由等比数列的通项公式即可得到所求;(2)求得cn= ![]() =(n+1)(
=(n+1)( ![]() )n﹣1 , 运用数列的求和方法:错位相减法,结合等比数列的求和公式可得Tn , 由不等式的性质即可得证.
)n﹣1 , 运用数列的求和方法:错位相减法,结合等比数列的求和公式可得Tn , 由不等式的性质即可得证.
【考点精析】本题主要考查了等比数列的通项公式(及其变式)和数列的前n项和的相关知识点,需要掌握通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系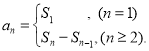 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图(1),在正方形SG1G2G3中,E、F分别是G1G2、G2G3的中点,D是EF的中点,现沿SE、SF及EF把这个正方形折成一个几何体如图(2),使G1、G2、G3三点重合于点G.证明: 
(1)G在平面SEF上的射影为△SEF的垂心;
(2)求二面角G﹣SE﹣F的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC=2 
(1)求证:AM⊥平面EBC
(2)(文)求三棱锥C﹣ABE的体积.
(3)(理)求二面角A﹣EB﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过双曲线C: ![]() =1(a>0,b>0)的中心的直线交双曲线于点A,B,在双曲线C上任取与点A,B不重合的点P,记直线PA,PB,AB的斜率分别为k1 , k2 , k,若k1k2>k恒成立,则离心率e的取值范围为( )
=1(a>0,b>0)的中心的直线交双曲线于点A,B,在双曲线C上任取与点A,B不重合的点P,记直线PA,PB,AB的斜率分别为k1 , k2 , k,若k1k2>k恒成立,则离心率e的取值范围为( )
A.1<e< ![]()
B.1<e≤ ![]()
C.e> ![]()
D.e≥ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为正数,其前n项的和为Sn , 且对任意的m,n∈N*,
都有(Sm+n+S1)2=4a2ma2n .
(1)求 ![]() 的值;
的值;
(2)求证:{an}为等比数列;
(3)已知数列{cn},{dn}满足|cn|=|dn|=an , p(p≥3)是给定的正整数,数列{cn},{dn}的前p项的和分别为Tp , Rp , 且Tp=Rp , 求证:对任意正整数k(1≤k≤p),ck=dk .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知长方体ABCD﹣A1B1C1D1中,E,M,N分别是BC,AE,CD1的中点,AD=AA1=a,AB=2a.求证:MN∥平面ADD1A1 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图已知抛物线![]() 的焦点坐标为
的焦点坐标为![]() ,过
,过![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,直线
两点,直线![]() 分别与直线
分别与直线![]() :
:![]() 相交于
相交于![]() 两点.
两点.

(1)求抛物线![]() 的方程;
的方程;
(2)证明△ABO与△MNO的面积之比为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com