【题目】如图已知抛物线
的焦点坐标为
，过
的直线交抛物线
于
两点，直线
分别与直线
：
相交于
两点．
(1)求抛物线
的方程；
(2)证明△ABO与△MNO的面积之比为定值．
【答案】（1）
；（2）证明过程详见解析.
【解析】
试题分析：本题主要考查抛物线、直线的方程，以及直线与抛物线的位置关系，突出解析几何的基本思想和方法的考查：如数形结合思想、坐标化方法等.第一问，利用抛物线的标准方程，利用焦点坐标求出
，代入即可；第二问，讨论直线
垂直和不垂直
轴2种情况，当直线垂直于轴时，2个三角形相似，面积比为定值，当直线不垂直于轴时，设出直线的方程，设出
四个点坐标，利用直线与抛物线相交列出方程组，消参得到方程，利用两根之积得
为定值，而面积比值与
有关，所以也为定值.
试题解析：（1）由焦点坐标为
可知
所以
,所以抛物线
的方程为 5分
（2）当直线垂直于
轴时，
与
相似，
所以
, 7分
当直线与轴不垂直时，设直线AB方程为
,
设
，
，
，
解
整理得
， 9分
所以, 10分
,
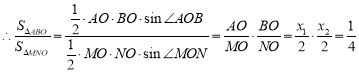综上
12分
科目：高中数学 来源： 题型：
【题目】已知各项均大于1的数列{an}满足：a1= 
，an+1= 
（an+ 
），（n∈N*），bn=log5 
．
（1）证明{bn}为等比数列，并求{bn}通项公式；
（2）若cn= 
，Tn为{cn}的前n项和，求证：Tn＜6．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设向量 
=（ 
sinx，sinx）， 
=（cosx，sinx），x∈[0， 
]
（1）若| |=| |，求x的值；
（2）设函数f（x）= ，求f（x）的值域．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线
的参数方程为
（
为参数），在以坐标原点为极点， 
轴的正半轴为极轴建立的极坐标系中，圆
的极坐标方程为
．
（1）求直线
被圆
截得的弦长；
（2）若点
的坐标为
，直线
与圆
交于
两点，求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}是递增的等比数列，且a1+a4=9，a2a3=8．
（1）求数列{an}的通项公式；
（2）设Sn为数列{an}的前n项和，bn= 
，求数列{bn}的前n项和Tn ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}满足a1+3a2+32a3+…+3n﹣1an= 
，n∈N+ ．
（1）求数列{an}的通项公式；
（2）设anbn=n，求数列{bn}的前n项和Sn ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学调查了某班全部45名同学参加书法社团和演讲社团的情况，数据如下表：（单位：人）
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 5 |
未参加演讲社团 | 2 | 30 |
（1）从该班随机选1名同学，求该同学至少参加一个社团的概率；
（2）在既参加书法社团又参加演讲社团的8名同学中，有5名男同学A1 ， A2 ， A3 ， A4 ， A5 ， 3名女同学B1 ， B2 ， B3 ． 现从这5名男同学和3名女同学中各随机选1人，求A1被选中且B1未被选中的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
已知平面直角坐标系
，以
为极点， 
轴的非负半轴为极轴建立极坐标系， 
点的极坐标为
，曲线
的参数方程为
（
为参数）.
（1）写出点
的直角坐标及曲线
的直角坐标方程；
（2）若
为曲线
上的动点，求
的中点
到直线
： 
的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
