Question

【题目】如图，已知长方体ABCD﹣A1B1C1D1中，E，M，N分别是BC，AE，CD1的中点，AD=AA1=a，AB=2a．求证：MN∥平面ADD1A1 ．

Answer 1

【答案】证明：以D为原点，分别以DA、DC、DD1为x轴、y轴、z轴建立空间直角坐标系，则A（a，0，0），B（a，2a，0），C（0，2a，0），D1（0，0，a），E（ a，2a，0），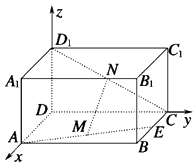

∵M、N分别为AE、CD1的中点，
∴M（ a，a，0），N（0，a， ）．
∴ =（﹣ a，0， ）．
取 =（0，1，0），
显然 =⊥平面A1D1DA，且 =0，
∴ ⊥ ．又MN平面ADD1A1 ．
∴MN∥平面ADD1A1
【解析】以D为原点，分别以DA、DC、DD1为x轴、y轴、z轴建立空间直角坐标系，求出 =（﹣ a，0， ）．平面ADD1A1的法向量 =（0，1，0），通过 =0，证明MN∥平面ADD1A1 ．
【考点精析】关于本题考查的直线与平面平行的判定，需要了解平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行才能得出正确答案．