
【题目】新高考![]() 最大的特点就是取消文理科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这
最大的特点就是取消文理科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这![]() 科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全理(选择物理、化学、生物)的选择是否与性别有关,觉得从某学校高一年级的
科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全理(选择物理、化学、生物)的选择是否与性别有关,觉得从某学校高一年级的![]() 名学生中随机抽取男生,女生各
名学生中随机抽取男生,女生各![]() 人进行模拟选科.经统计,选择全理的人数比不选全理的人数多
人进行模拟选科.经统计,选择全理的人数比不选全理的人数多![]() 人.
人.
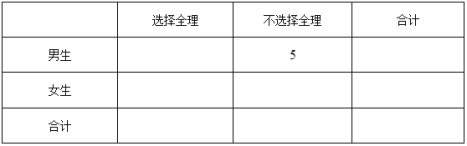
(1)请完成下面的![]() 列联表;
列联表;
(2)估计有多大把握认为选择全理与性别有关,并说明理由;
(3)现从这![]() 名学生中已经选取了男生
名学生中已经选取了男生![]() 名,女生
名,女生![]() 名进行座谈,从中抽取
名进行座谈,从中抽取![]() 名代表作问卷调查,求至少抽到一名女生的概率.
名代表作问卷调查,求至少抽到一名女生的概率.
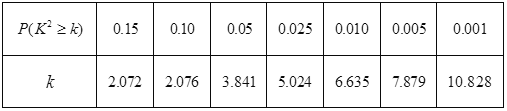
附: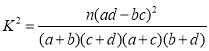 ,其中
,其中![]() .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图是甲、乙、丙三个企业的产品成本(单位:万元)及其构成比例,则下列判断正确的是( )

A. 乙企业支付的工资所占成本的比重在三个企业中最大
B. 由于丙企业生产规模大,所以它的其他费用开支所占成本的比重也最大
C. 甲企业本着勤俭创业的原则,将其他费用支出降到了最低点
D. 乙企业用于工资和其他费用支出额比甲丙都高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,其中
,其中![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 单调递增区间;
单调递增区间;
(2)求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(3)是否存在实数![]() 的值,使得
的值,使得![]() 在
在![]() 上有最大值或最小值,若存在,求出实数
上有最大值或最小值,若存在,求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,![]() 是等腰三角形,且
是等腰三角形,且![]() .四边形ABCD是直角梯形,
.四边形ABCD是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
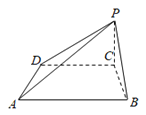
(1)求证:![]() 平面PDC.
平面PDC.
(2)请在图中所给的五个点P,A,B,C,D中找出两个点,使得这两点所在直线与直线BC垂直,并给出证明.
(3)当平面![]() 平面ABCD时,求直线PC与平面PAB所成角的正弦值.
平面ABCD时,求直线PC与平面PAB所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() 是正三角形,
是正三角形,![]() ,
,![]() .
.
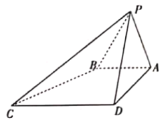
(1)求平面![]() 与平面
与平面![]() 所成的锐二面角的大小;
所成的锐二面角的大小;
(2)点![]() 为线段
为线段![]() 上的一动点,设异面直线
上的一动点,设异面直线![]() 与直线
与直线![]() 所成角的大小为
所成角的大小为![]() ,当
,当![]() 时,试确定点
时,试确定点![]() 的位置.
的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com